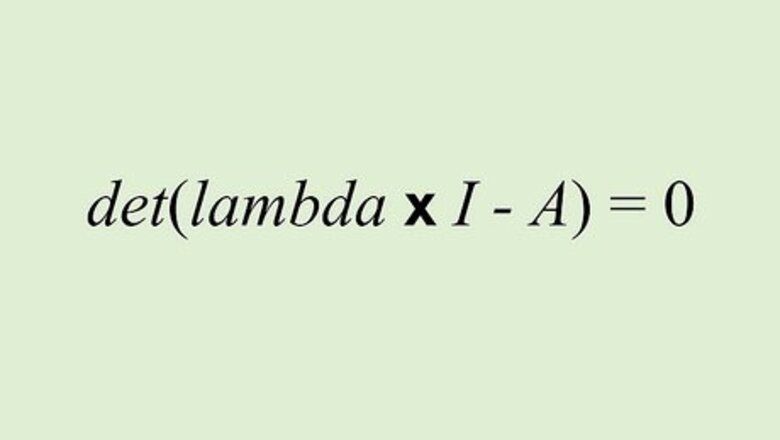
views
- Find the eigenvalues of your given matrix.
- Use the eigenvalues to get the eigenvectors.
- Apply the diagonalization equation using the eigenvectors to find the diagonal matrix.
- Note that not all matrices can be diagonalized.
Find the Eigenvalues
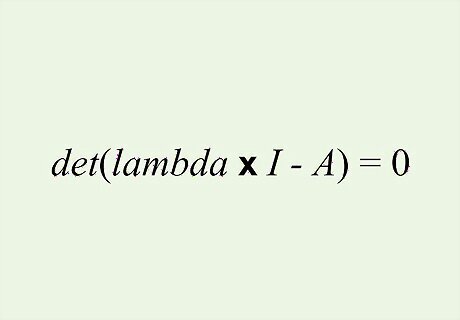
Recall the equation for finding eigenvalues. Eigenvalues are the scalar value associated with an eigenvector, represented by the symbol lambda (λ). To find eigenvalues, use the following equation: d e t ( l a m b d a ∗ I − A ) = 0 {\displaystyle det(lambda*I-A)=0} {\displaystyle det(lambda*I-A)=0} In other words, the determinant of lambda times the identity matrix minus the given transformation matrix.
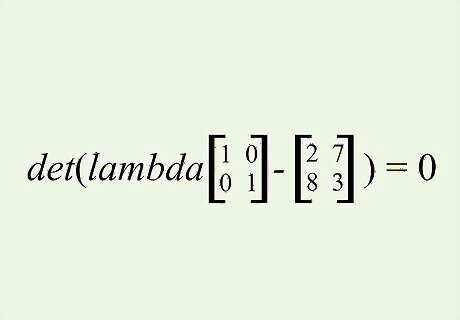
Set up the determinant equation. Here is an example for a 2 by 2 matrix: d e t ( l a m b d a [ 1 0 0 1 ] − [ 2 7 8 3 ] ) = 0 {\displaystyle det(lambda{\begin{bmatrix}1&0\\0&1\end{bmatrix}}-{\begin{bmatrix}2&7\\8&3\end{bmatrix}})=0} {\displaystyle det(lambda{\begin{bmatrix}1&0\\0&1\end{bmatrix}}-{\begin{bmatrix}2&7\\8&3\end{bmatrix}})=0}
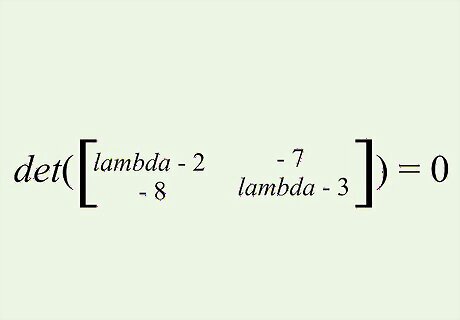
Simplify the determinant equation. The equation simplifies to: d e t ( [ l a m b d a − 2 − 7 − 8 l a m b d a − 3 ] ) = 0 {\displaystyle det({\begin{bmatrix}lambda-2&-7\\-8&lambda-3\end{bmatrix}})=0} {\displaystyle det({\begin{bmatrix}lambda-2&-7\\-8&lambda-3\end{bmatrix}})=0}

Solve for the determinant. To do so in a 2 by 2 matrix, multiply the top-left value and the bottom-right value, then subtract the product of the top-right value and bottom-left value. We also have a guide for finding the determinant for 3x3 matrices. Continuing our example: ( l a m b d a − 2 ) ( l a m b d a − 3 ) − ( − 8 ) ( − 7 ) = 0 {\displaystyle (lambda-2)(lambda-3)-(-8)(-7)=0} {\displaystyle (lambda-2)(lambda-3)-(-8)(-7)=0} l a m b d a 2 − 5 l a m b d a − 50 = 0 {\displaystyle lambda^{2}-5lambda-50=0} {\displaystyle lambda^{2}-5lambda-50=0} l a m b d a = − 5 {\displaystyle lambda=-5} {\displaystyle lambda=-5} and l a m b d a = 10 {\displaystyle lambda=10} {\displaystyle lambda=10} These two values are the eigenvalues.
Find the Eigenvectors
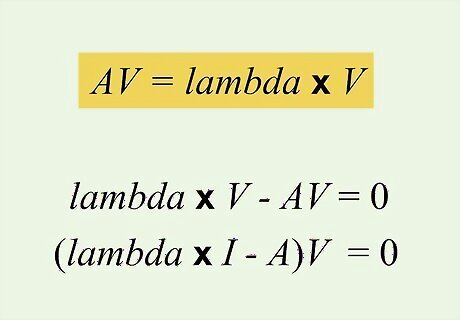
Use the equation to find eigenvectors. Recall that the equation to find eigenvectors for a given lambda: A V = l a m b d a ∗ V {\displaystyle AV=lambda*V} {\displaystyle AV=lambda*V} In other words, a given transformation matrix (A) times the eigenvector (V) equals the eigenvalue (lambda) times the eigenvector (V). This can be rewritten as: l a m b d a ∗ V − A V = 0 {\displaystyle lambda*V-AV=0} {\displaystyle lambda*V-AV=0} ( l a m b d a ∗ I − A ) V = 0 {\displaystyle (lambda*I-A)V=0} {\displaystyle (lambda*I-A)V=0} Where I is the identity matrix.
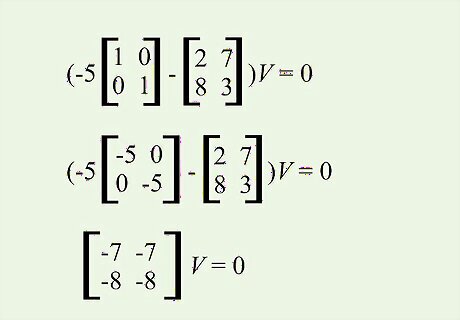
Plug in an eigenvalue to the equation. For example, using the eigenvalue lambda = -5 from our problem: ( − 5 [ 1 0 0 1 ] − [ 2 7 8 3 ] ) V = 0 {\displaystyle (-5{\begin{bmatrix}1&0\\0&1\end{bmatrix}}-{\begin{bmatrix}2&7\\8&3\end{bmatrix}})V=0} {\displaystyle (-5{\begin{bmatrix}1&0\\0&1\end{bmatrix}}-{\begin{bmatrix}2&7\\8&3\end{bmatrix}})V=0} ( [ − 5 0 0 − 5 ] − [ 2 7 8 3 ] ) V = 0 {\displaystyle ({\begin{bmatrix}-5&0\\0&-5\end{bmatrix}}-{\begin{bmatrix}2&7\\8&3\end{bmatrix}})V=0} {\displaystyle ({\begin{bmatrix}-5&0\\0&-5\end{bmatrix}}-{\begin{bmatrix}2&7\\8&3\end{bmatrix}})V=0} [ − 7 − 7 − 8 − 8 ] V = 0 {\displaystyle {\begin{bmatrix}-7&-7\\-8&-8\end{bmatrix}}V=0} {\displaystyle {\begin{bmatrix}-7&-7\\-8&-8\end{bmatrix}}V=0}
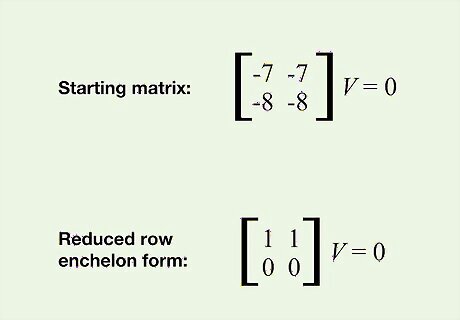
Find the reduced row echelon form. Use elementary row operations to get the reduced row echelon form of the new matrix. Continuing our example: Our starting matrix: [ − 7 − 7 − 8 − 8 ] V = 0 {\displaystyle {\begin{bmatrix}-7&-7\\-8&-8\end{bmatrix}}V=0} {\displaystyle {\begin{bmatrix}-7&-7\\-8&-8\end{bmatrix}}V=0} The matrix in reduced row echelon form: [ 1 1 0 0 ] V = 0 {\displaystyle {\begin{bmatrix}1&1\\0&0\end{bmatrix}}V=0} {\displaystyle {\begin{bmatrix}1&1\\0&0\end{bmatrix}}V=0}

Find the eigenvector. To do so: Our starting matrix equation: [ 1 1 0 0 ] ∗ [ V 1 V 2 ] = [ 0 0 ] {\displaystyle {\begin{bmatrix}1&1\\0&0\end{bmatrix}}*{\begin{bmatrix}V_{1}\\V_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}} {\displaystyle {\begin{bmatrix}1&1\\0&0\end{bmatrix}}*{\begin{bmatrix}V_{1}\\V_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}} Writing the matrix as a linear equation: V 1 + V 2 = 0 {\displaystyle V_{1}+V_{2}=0} {\displaystyle V_{1}+V_{2}=0} V 1 = − V 2 {\displaystyle V_{1}=-V_{2}} {\displaystyle V_{1}=-V_{2}} Write the components as an eigenvector: [ − 1 1 ] {\displaystyle {\begin{bmatrix}-1\\1\end{bmatrix}}} {\displaystyle {\begin{bmatrix}-1\\1\end{bmatrix}}}

Repeat the above eigenvector process for any other eigenvalues. You’ll need the eigenvectors for each of the eigenvalues to diagonalize the matrix. For example, repeating the process for lambda = 10 yields the eigenvector: [ 7 8 ] {\displaystyle {\begin{bmatrix}7\\8\end{bmatrix}}} {\displaystyle {\begin{bmatrix}7\\8\end{bmatrix}}}
Diagonalize the Matrix
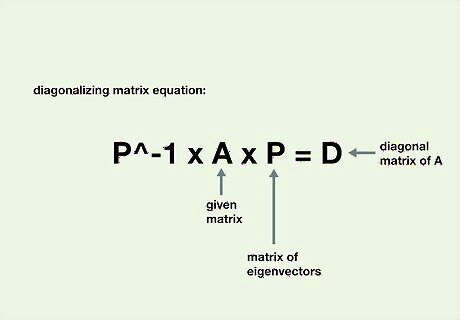
Note the equation for diagonalizing a matrix. The equation is: P^-1 * A * P = D Where P is the matrix of eigenvectors, A is the given matrix, and D is the diagonal matrix of A.
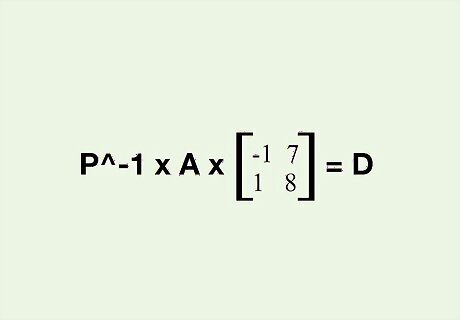
Write P, the matrix of eigenvectors. For our example with two eigenvectors, P would be: [ − 1 7 1 8 ] {\displaystyle {\begin{bmatrix}-1&7\\1&8\end{bmatrix}}} {\displaystyle {\begin{bmatrix}-1&7\\1&8\end{bmatrix}}} Where the first column is the eigenvector of lambda = -5, and the second column is the eigenvector for lambda = 10.
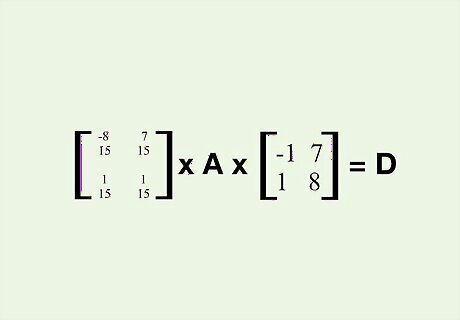
Find the inverse of P. For our example, the inverse of P (P^-1) is: [ − 8 / 15 7 / 15 1 / 15 1 / 15 ] {\displaystyle {\begin{bmatrix}-8/15&7/15\\1/15&1/15\end{bmatrix}}} {\displaystyle {\begin{bmatrix}-8/15&7/15\\1/15&1/15\end{bmatrix}}} Check out our expert guide to finding the inverse of a 3x3 matrix if you need a refresher!
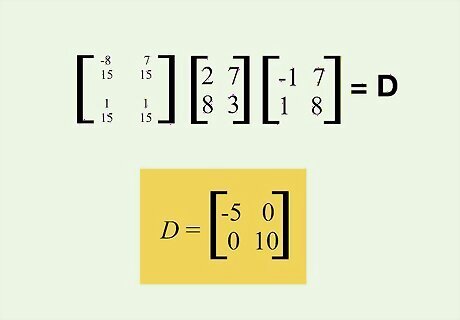
Solve for the diagonal matrix D. Use the equation P^-1 * A * P = D to diagonalize the matrix A. Continuing our example: [ − 8 / 15 7 / 15 1 / 15 1 / 15 ] [ 2 7 8 3 ] [ − 1 1 7 8 ] = D {\displaystyle {\begin{bmatrix}-8/15&7/15\\1/15&1/15\end{bmatrix}}{\begin{bmatrix}2&7\\8&3\end{bmatrix}}{\begin{bmatrix}-1&1\\7&8\end{bmatrix}}=D} {\displaystyle {\begin{bmatrix}-8/15&7/15\\1/15&1/15\end{bmatrix}}{\begin{bmatrix}2&7\\8&3\end{bmatrix}}{\begin{bmatrix}-1&1\\7&8\end{bmatrix}}=D} D = [ − 5 0 0 10 ] {\displaystyle D={\begin{bmatrix}-5&0\\0&10\end{bmatrix}}} {\displaystyle D={\begin{bmatrix}-5&0\\0&10\end{bmatrix}}} You’re done! You have diagonalized a matrix. For more linear algebra info, check out how to divide matrices and how to transpose a matrix.


















Comments
0 comment