views
Creating a Trig Table
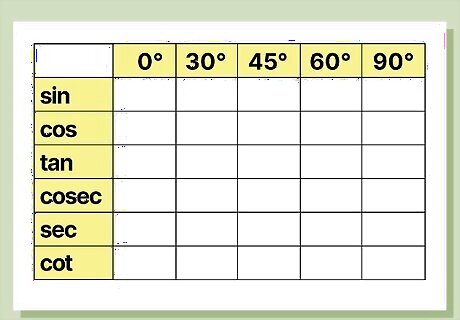
Draw a blank trigonometry table. Creating a trigonometric table can help you remember key trig formulas. Design your table to have 6 rows and 6 columns. In the 1st column, write down the key trigonometric ratios (sine, cosine, tangent, cosecant, secant, and cotangent). In the 1st row, write down the angles you’ll most commonly be using in trigonometry (0°, 30°, 45°, 60°, 90°). Sine, cosine, and tangent are the more commonly used trigonometric ratios, although you should also learn cosecant, secant, and cotangent to have a more in-depth knowledge of trigonometry and the trigonometric table.
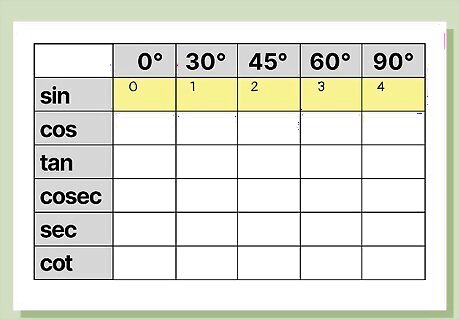
Number your table’s columns in ascending order, starting at 0. Once you’ve created your 6 rows and columns, assign each column a number from 0-4. The number for the 0° column should be 0, the number for 30° should be 1, 45° should be 2, 60° should be 3, and 90° should be 4.
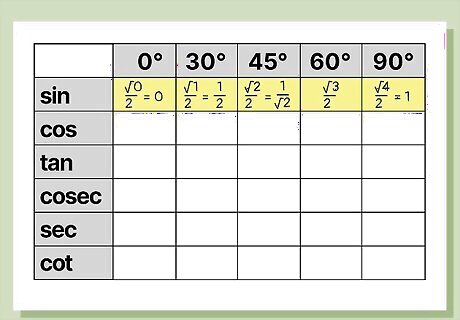
Use √x/2 to find the values for your table’s sine row. Plug in each column’s number into the formula √x/2. Use this formula to calculate the sine values for 0°, 30°, 45°, 60°, and 90° and write those values in your table. For example, for the first entry in the sine column (sin 0°), set x to equal 0 and plug it into the expression √x/2. This will give you √0/2, which can be simplified to 0/2 and then finally to 0. Plugging the angles into the expression √x/2 in this way, the remaining entries in the sine row are √1/2 (which can be simplified to ½, since the square root of 1 is 1), √2/2 (which can be simplified to 1/√2, since √2/2 is also equal to (1 x √2)/(√2 x √2) and in this fraction, the “√2” in the numerator and a “√2” in the denominator cancel each other out, leaving 1/√2), √3/2, and √4/2 (which can be simplified to 1, since the square root of 4 is 2 and 2/2 = 1). Once the sine row is filled, it’ll be a lot easier to fill in the remaining rows.
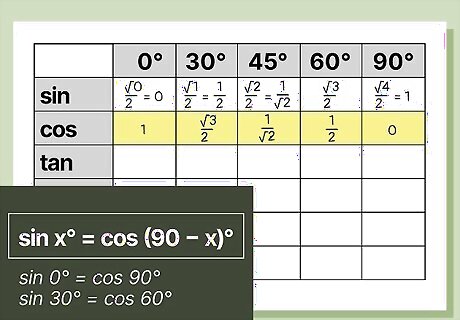
Place the sine row entries in the cosine row in reverse order. Mathematically speaking, sin x° = cos (90-x)° for any x value. Thus, to fill in the cosine row, simply take the entries in the sine row and place them in reverse order in the cosine row. Fill in the cosine row so that the value for the sine of 90° is also used as the value for the cosine of 0°, the value for the sine of 60° is used as the value for the cosine of 30°, and so on. For example, since 1 is the value placed in the final entry in the sine column (sine of 90°), this value will be placed in the 1st entry for the cosine column (cosine of 0°). Once filled, the values in the cosine row should be 1, √3/2, 1/√2, ½, and 0.
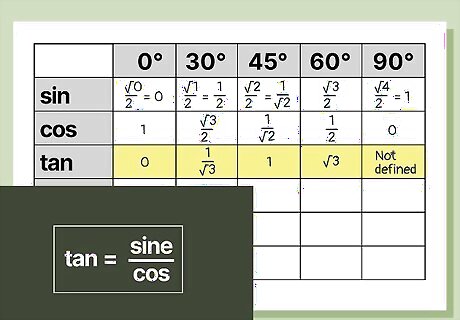
Divide your sine values by the cosine values to fill the tangent row. Simply speaking, tangent = sine/cosine. Therefore, for every angle, take its sine value and divide it by its cosine value to calculate the corresponding tangent value. To take 30° as an example: tan 30° = sin 30° / cos 30° = (√1/2) / (√3/2) = 1/√3. The entries of your tangent row should be 0, 1/√3, 1, √3, and undefined for 90°. The tangent of 90° is undefined because sin 90° / cos 90° = 1/0 and division by 0 is always undefined.
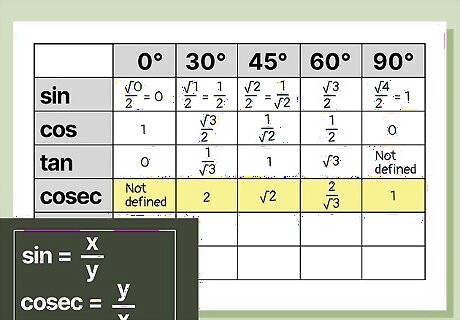
Reverse the entries in the sine row to find the cosecant of an angle. Starting from the bottom row (or denominator) of the sine row, take the sine values you’ve already calculated and place them in reverse order (above the numerator) in the cosecant row. This works because the cosecant of an angle is equal to the inverse of the sine of that angle. For instance, use the sine of 90° to fill in the entry for the cosecant of 0°, the sine of 60° for the cosecant of 30°, and so on.
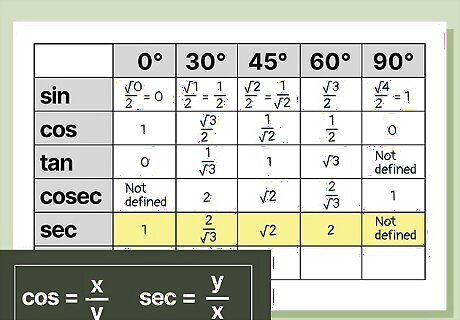
Reverse the entries of the cosine row to fill out the secant row. Starting from the cosine of 90°, enter the values from the cosine row in the secant row, such that value for the cosine of 90° is used as the value for the secant of 0°, the value for the cosine of 60° is used as the value for the secant of 30°, and so on. This is mathematically valid because the inverse of the cosine of an angle is equal to that angle’s secant.
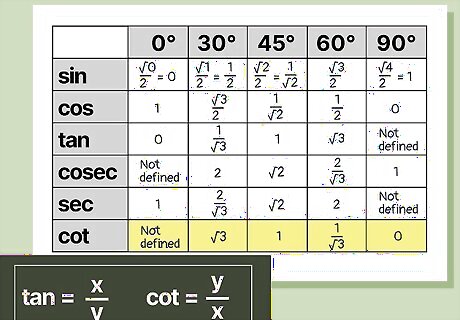
Fill the cotangent row by reversing the values from the tangent row. Take the value for the tangent of 90° and place it in the entry space for the cotangent of 0° in your cotangent row. Do the same for the tangent of 60° and the cotangent of 30°, the tangent of 45° and the cotangent of 45°, and so on, until you’ve filled in the cotangent row by inverting the order of entries in the tangent row. This works because the cotangent of an angle is equal to the inversion of the tangent of an angle. You can also find the cotangent of an angle by dividing its cosine by its sine.
Using a Mnemonic Device
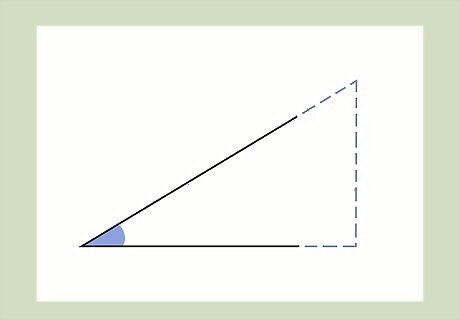
Draw a right triangle around the angle you’re working with. For an easy way to memorize the formulas of trigonometric ratios, start by extending 2 straight lines out from the sides of the angle. Then, draw a third line perpendicular to 1 of these 2 lines to create a right angle. Continue drawing this perpendicular line towards the other of the 2 original lines until they intersect, thereby creating a right triangle around the angle you’re working with. If you’re calculating sine, cosine, or tangent in the context of a math class, it’s likely you’ll already be working with a right triangle. Right triangles are a key part of remembering right-angled trigonometry and trig in general.
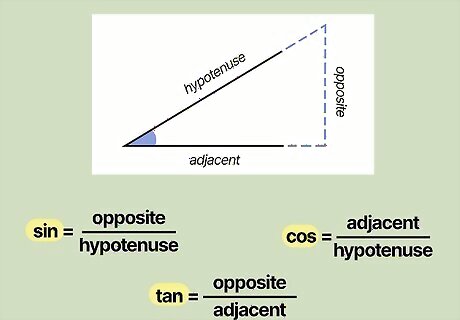
Calculate sine, cosine, or tangent by using the sides of the triangle. The sides of the triangle can be identified in relation to the angle as the “opposite” (the side opposite of the angle), the “adjacent” (the side next to the angle other than the hypotenuse), and the “hypotenuse” (the side opposite the right angle of the triangle). Sine, cosine, and tangent can all be expressed as different ratios of these sides. The sine of an angle is equal to the opposite side divided by the hypotenuse. The cosine of an angle is equal to the adjacent side divided by the hypotenuse. The tangent of an angle is equal to the opposite side divided by the adjacent side. For example, to determine the sine of a 35° angle, divide the length of the opposite side of the triangle by the hypotenuse. If the opposite side’s length was 2.8 and the hypotenuse was 4.9, then the sine of the angle would be 2.8/4.9, which is equal to 0.57.
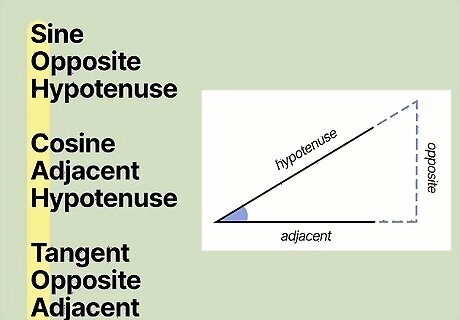
Use a mnemonic device to remember ratios for sin, cos, and tan. The most commonly used acronym to remember trigonometric ratios is SOHCAHTOA, which stands for “Sine Opposite Hypotenuse, Cosine Adjacent Hypotenuse, Tangent Opposite Adjacent.” To better remember this acronym, spell out a mnemonic phrase with these letters like “She Offered Her Child A Heaping Teaspoon Of Applesauce.”
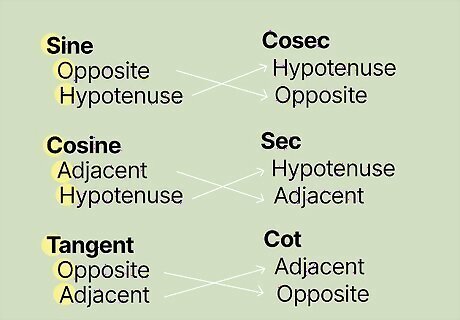
Inverse the sine, cosine, or tangent to find their reciprocal ratios. To calculate cosecant, secant, and cotangent, simply invert the ratios of each triangle side using SOHCAHTOA. Because cosecant is the inverse of sine, it is equal to the hypotenuse divided by the opposite side. The secant of an angle is equal to the hypotenuse divided by the adjacent side, and the cotangent of an angle is equal to the adjacent side divided by the opposite side. For example, if you wanted to find the cosecant of a 35°, with an opposite side length of 2.8 and a hypotenuse of 4.9, you would divide 4.9 by 2.8 to get a cosecant of 1.75.

















Comments
0 comment