2 Different Ways to Find a Circle’s Arc Length

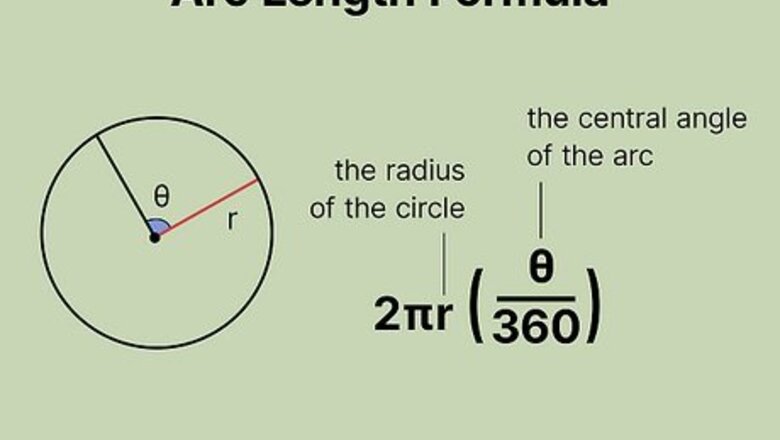
• When the circle’s central angle is measured in degrees, use the formula ${\displaystyle {\text{arc length}}=2\pi (r)({\frac {\theta }{360}})}$.
• If the central angle is in radians, use the formula ${\displaystyle {\text{arc length}}=\theta (r)}$.
• Plug in the circle’s radius and the central angle’s measurement to solve either formula.

Solving When the Central Angle is in Degrees

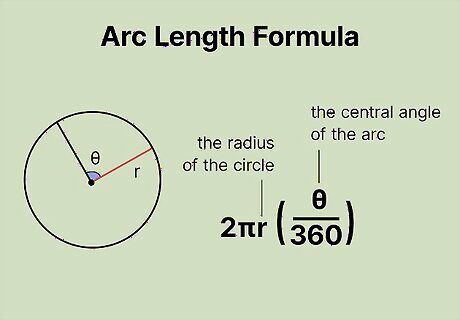
Set up the formula for arc length. The formula is arc length = 2 π ( r ) ( θ 360 ) {\displaystyle {\text{arc length}}=2\pi (r)({\frac {\theta }{360}})} {\text{arc length}}=2\pi (r)({\frac {\theta }{360}}), where r {\displaystyle r} r equals the radius of the circle and θ {\displaystyle \theta } \theta equals the measurement of the arc’s central angle, in degrees.

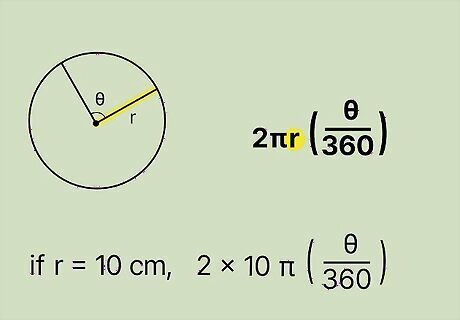
Plug the length of the circle’s radius into the formula. This information is typically given to you in a problem. Otherwise, measure the circle’s radius with a ruler or protractor. Simply substitute the radius’ value for the variable r {\displaystyle r} r. For example, if the circle’s radius is 10 cm, set up the formula like this: arc length = 2 π ( 10 ) ( θ 360 ) {\displaystyle {\text{arc length}}=2\pi (10)({\frac {\theta }{360}})} {\text{arc length}}=2\pi (10)({\frac {\theta }{360}}).

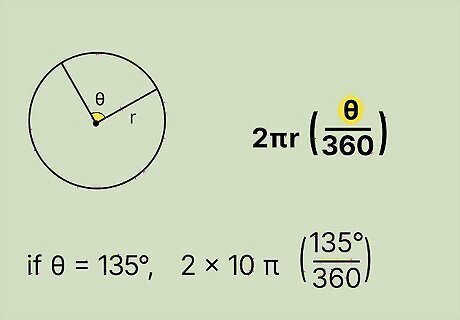
Insert the value of the arc’s central angle into the formula. Typically, the problem you’re working on provides this information. Make sure to convert the angle to degrees if it’s currently in radians. Then, substitute the central angle’s measurement for θ {\displaystyle \theta } \theta in the formula. For example, if the arc’s central angle is 135 degrees, your formula now looks like: arc length = 2 π ( 10 ) ( 135 360 ) {\displaystyle {\text{arc length}}=2\pi (10)({\frac {135}{360}})} {\text{arc length}}=2\pi (10)({\frac {135}{360}}).

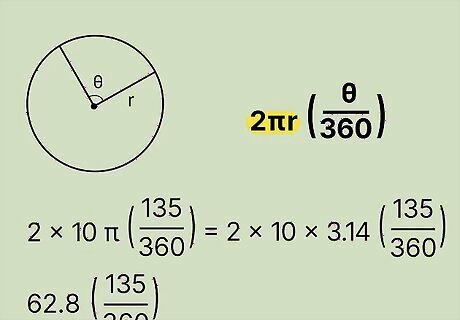
Multiply the radius by 2 π {\displaystyle 2\pi } 2\pi . If you are not using a calculator, use the approximation π = 3.14 {\displaystyle \pi =3.14} \pi =3.14 for your calculations. Rewrite the formula using this new value, which represents the circle’s circumference. For example, your formula now looks like: arc length = 2 π ( 10 ) ( 135 360 ) {\displaystyle {\text{arc length}}=2\pi (10)({\frac {135}{360}})} {\text{arc length}}=2\pi (10)({\frac {135}{360}}) = 2 ( 3.14 ) ( 10 ) ( 135 360 ) {\displaystyle =2(3.14)(10)({\frac {135}{360}})} {\displaystyle =2(3.14)(10)({\frac {135}{360}})} = ( 62.8 ) ( 135 360 ) {\displaystyle =(62.8)({\frac {135}{360}})} {\displaystyle =(62.8)({\frac {135}{360}})}

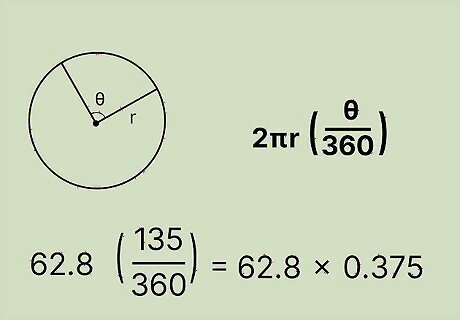
Divide the arc’s central angle by 360 degrees. Since a circle has 360 degrees total, dividing the central angle by 360 degrees gives you the portion of the circle that the sector represents. Using this information, find what portion of the circumference the arc length represents. For example, simplify the formula to get: arc length = ( 62.8 ) ( 135 360 ) {\displaystyle {\text{arc length}}=(62.8)({\frac {135}{360}})} {\displaystyle {\text{arc length}}=(62.8)({\frac {135}{360}})} = ( 62.8 ) ( .375 ) {\displaystyle =(62.8)(.375)} {\displaystyle =(62.8)(.375)}

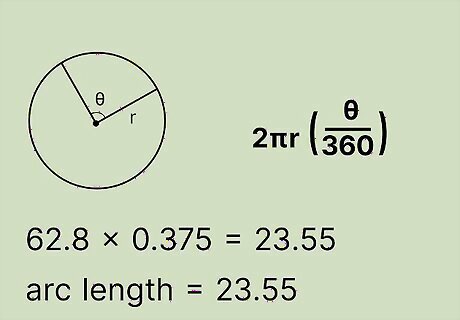
Multiply the two numbers together. This gives you the length of the arc. Solve the formula: arc length = ( 62.8 ) ( .375 ) = 23.55 {\displaystyle {\text{arc length}}=(62.8)(.375)=23.55} {\displaystyle {\text{arc length}}=(62.8)(.375)=23.55}So, the arc length of a circle with a radius of 10 cm and a central angle of 135 degrees is about 23.55 cm.

Solving When the Central Angle is in Radians

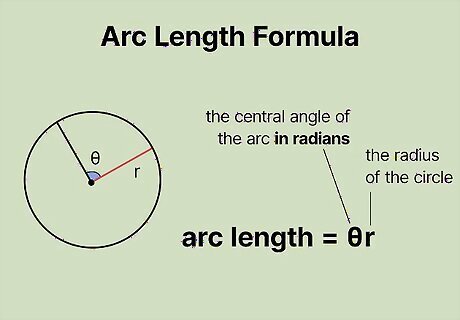
Set up the formula for arc length. The formula is arc length = θ ( r ) {\displaystyle {\text{arc length}}=\theta (r)} {\text{arc length}}=\theta (r), where θ {\displaystyle \theta } \theta equals the arc’s central angle in radians, and r {\displaystyle r} r equals the length of the circle’s radius.

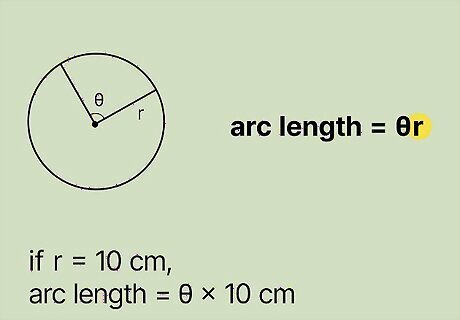
Plug the length of the circle’s radius into the formula. The math problem you’re working on typically provides this information. Just substitute the length of the radius for the variable r {\displaystyle r} r. For example, if the circle’s radius is 10 cm, your formula looks like this: arc length = θ ( 10 ) {\displaystyle {\text{arc length}}=\theta (10)} {\text{arc length}}=\theta (10).

Plug the measurement of the arc’s central angle into the formula. When using this formula, the arc’s central angle needs to be in radians. If the central angle is in degrees, just convert it into radians. For example, if the arc’s central angle is 2.36 radians, your formula now looks like this: arc length = 2.36 ( 10 ) {\displaystyle {\text{arc length}}=2.36(10)} {\text{arc length}}=2.36(10).

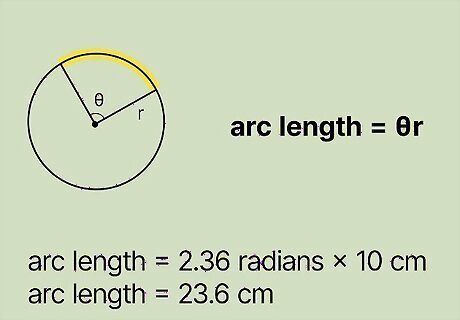
Multiply the radius by the arc’s central angle. The product gives you the length of the arc. For example: arc length = 2.36 ( 10 ) = 23.6 {\displaystyle {\text{arc length}}=2.36(10)=23.6} {\displaystyle {\text{arc length}}=2.36(10)=23.6}So, the length of an arc of a circle with a radius of 10 cm and a central angle of 23.6 radians, is about 23.6 cm.