How to Calculate the Mass of a Sphere

Finding the Volume of a Sphere

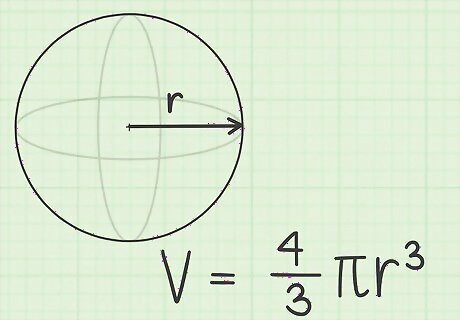
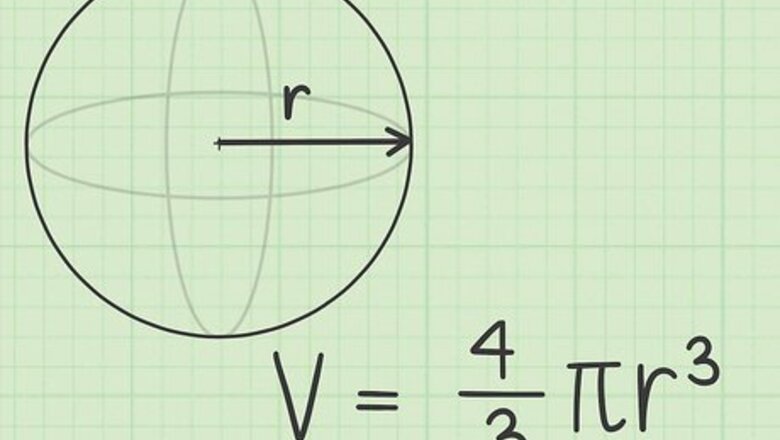
Recall the formula for a sphere’s volume. A sphere is a circular solid in three dimensions. The primary formula for the volume of a sphere is: Volume = 4 3 π r 3 {\displaystyle {\text{Volume}}={\frac {4}{3}}\pi r^{3}} {\text{Volume}}={\frac {4}{3}}\pi r^{3} π = 3.14 {\displaystyle \pi =3.14} \pi =3.14 r = radius {\displaystyle r={\text{radius}}} r={\text{radius}}

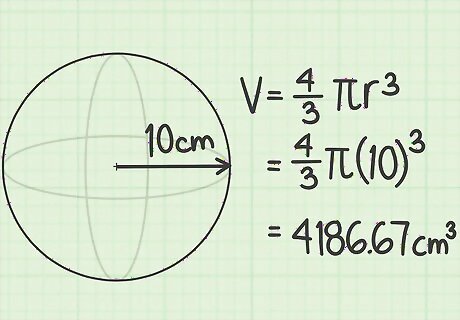
Find the volume of a sphere if you know the radius. The radius of a sphere is the measure from the center of the sphere to the outer edge. If you are given a problem to calculate volume, you will probably be given the radius. Otherwise, the radius can be difficult to measure because you cannot accurately reach the center of a solid object. Suppose you are told that a sphere exists with a radius of 10 cm. Find the volume as follows: Volume = 4 3 π r 3 {\displaystyle {\text{Volume}}={\frac {4}{3}}\pi r^{3}} {\text{Volume}}={\frac {4}{3}}\pi r^{3} Volume = 4 3 ∗ ( 3.14 ) ∗ 10 3 {\displaystyle {\text{Volume}}={\frac {4}{3}}*(3.14)*10^{3}} {\text{Volume}}={\frac {4}{3}}*(3.14)*10^{3} Volume = 4.18667 ∗ 1000 {\displaystyle {\text{Volume}}=4.18667*1000} {\text{Volume}}=4.18667*1000 Volume = 4186.67 cm 3 {\displaystyle {\text{Volume}}=4186.67{\text{cm}}^{3}} {\text{Volume}}=4186.67{\text{cm}}^{3}

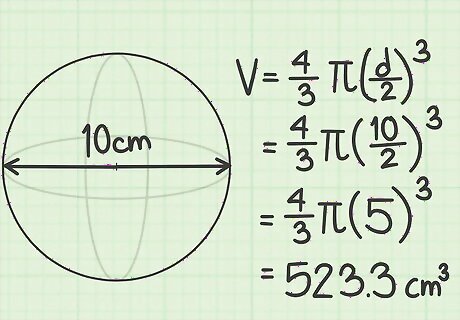
Find the volume if given the diameter. Alternatively, a given situation may provide you with the diameter of a sphere. The diameter is equal to double the radius. In more concrete terms, the diameter is the distance that passes from one edge of the sphere through the center to the opposite edge. To calculate volume beginning with the diameter (d), revise the formula as follows: Volume = 4 3 π ( d 2 ) 3 {\displaystyle {\text{Volume}}={\frac {4}{3}}\pi ({\frac {d}{2}})^{3}} {\text{Volume}}={\frac {4}{3}}\pi ({\frac {d}{2}})^{3} As an example of this calculation, find the volume of a sphere whose diameter is 10 cm. Volume = 4 3 π ( d 2 ) 3 {\displaystyle {\text{Volume}}={\frac {4}{3}}\pi ({\frac {d}{2}})^{3}} {\text{Volume}}={\frac {4}{3}}\pi ({\frac {d}{2}})^{3} Volume = 4 3 π ( 10 2 ) 3 {\displaystyle {\text{Volume}}={\frac {4}{3}}\pi ({\frac {10}{2}})^{3}} {\text{Volume}}={\frac {4}{3}}\pi ({\frac {10}{2}})^{3} Volume = 4 3 ∗ ( 3.14 ) ∗ ( 5 3 ) {\displaystyle {\text{Volume}}={\frac {4}{3}}*(3.14)*(5^{3})} {\text{Volume}}={\frac {4}{3}}*(3.14)*(5^{3}) Volume = 4.18667 ∗ 125 {\displaystyle {\text{Volume}}=4.18667*125} {\text{Volume}}=4.18667*125 Volume = 523.3 cm 3 {\displaystyle {\text{Volume}}=523.3{\text{cm}}^{3}} {\text{Volume}}=523.3{\text{cm}}^{3}

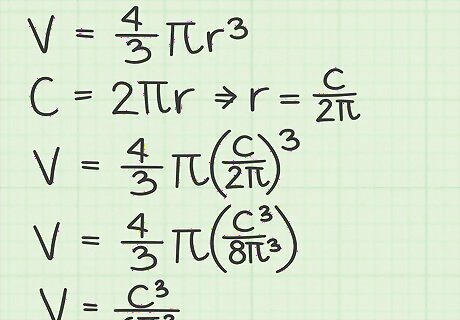
Revise the formula if you know the circumference. The circumference of a sphere is probably the easiest one for you to measure directly. You can use a tape measure, wrap it carefully around the widest part of the sphere, and take the measurement. Alternatively, you may be provided the circumference in a stated problem. To find the volume beginning with the circumference (C), revise the formula as follows: Volume = 4 3 π r 3 {\displaystyle {\text{Volume}}={\frac {4}{3}}\pi r^{3}} {\text{Volume}}={\frac {4}{3}}\pi r^{3} Volume = 4 3 π ∗ ( C 2 π ) 3 {\displaystyle {\text{Volume}}={\frac {4}{3}}\pi *({\frac {C}{2\pi }})^{3}} {\text{Volume}}={\frac {4}{3}}\pi *({\frac {C}{2\pi }})^{3} Volume = 4 3 π ∗ ( C 3 8 π 3 ) {\displaystyle {\text{Volume}}={\frac {4}{3}}\pi *({\frac {C^{3}}{8\pi ^{3}}})} {\text{Volume}}={\frac {4}{3}}\pi *({\frac {C^{3}}{8\pi ^{3}}}) Volume = C 3 6 π 2 {\displaystyle {\text{Volume}}={\frac {C^{3}}{6\pi ^{2}}}} {\text{Volume}}={\frac {C^{3}}{6\pi ^{2}}}

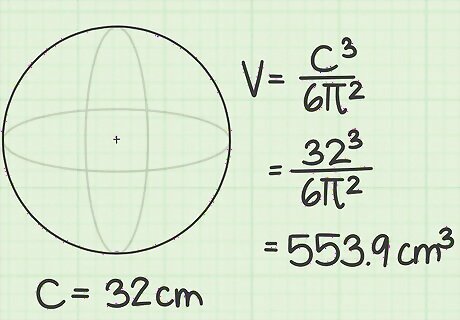
Calculate the volume if you know the circumference. Suppose you are given a sphere and you measure the circumference to be 32 cm. Find its volume: Volume = C 3 6 π 2 {\displaystyle {\text{Volume}}={\frac {C^{3}}{6\pi ^{2}}}} {\text{Volume}}={\frac {C^{3}}{6\pi ^{2}}} Volume = 32 3 6 ∗ 3.14 2 {\displaystyle {\text{Volume}}={\frac {32^{3}}{6*3.14^{2}}}} {\text{Volume}}={\frac {32^{3}}{6*3.14^{2}}} Volume = 32 , 768 59.158 {\displaystyle {\text{Volume}}={\frac {32,768}{59.158}}} {\text{Volume}}={\frac {32,768}{59.158}} Volume = 553.9 cm 3 {\displaystyle {\text{Volume}}=553.9{\text{cm}}^{3}} {\text{Volume}}=553.9{\text{cm}}^{3}

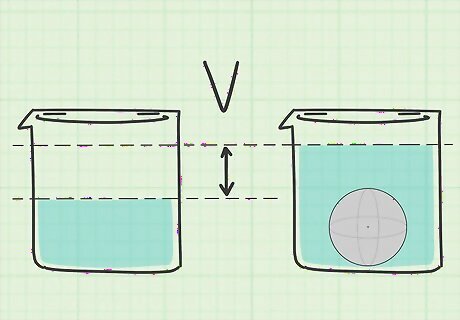
Measure volume by displacement. A final, practical method for measuring volume is to submerge the sphere into water. You need to have a beaker large enough to hold the sphere, with accurate volume measurement markings. Pour enough water into the beaker to cover the sphere. Make note of the measurement. Place the sphere into the water. Notice that the water level rises. Make note of the new measurement. Subtract the first measurement from the second. The result is the volume of the sphere. For example, suppose your water level rises from 100 ml to 625 ml when you submerge the sphere. The volume is therefore 525 ml. Note that 1 ml=1 cm.

Calculating Mass from Volume

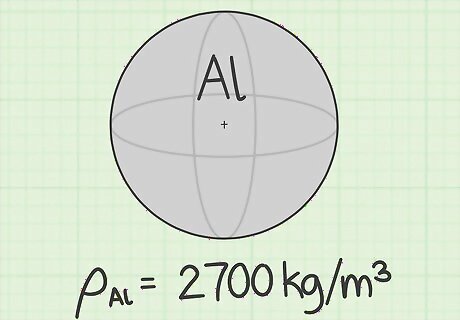
Find the density. To calculate mass from volume, you must know the density of the object. Different materials have different densities. Consider a sphere made of styrofoam, for example, and compare its weight to a sphere the same size made of iron. Iron has a much greater density and will therefore have a greater mass. You can find densities of many solid materials by looking up density tables online, in textbooks or in other industry catalogs. For example, here are the recorded densities of some solid materials: Aluminum = 2700 kg/m Butter = 870 kg/m Lead = 11,350 kg/m Pressed wood = 190 kg/m

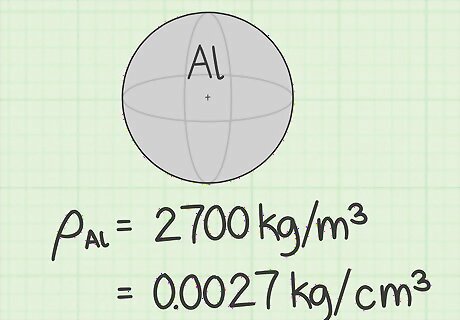
Convert the units as needed. The units you used in calculating volume must match the volume units in the density measurement. If they do not, then you must convert them. All of the examples in the previous section resulted in volumes measured in cubic centimeters. However, the cited density table provides densities based on cubic meters. Because there are 100 centimeters in a meter, there are 10 cubic centimeters in a cubic meter. Divide the given densities by 10 to represent the density in units of kg/cm. (You can do this most easily by just moving the decimal point 6 spaces to the left.) For the four sample materials, the converted densities are as follows: Aluminum = 2700 kg/m = 0.0027 kg/cm Butter = 870 kg/m = 0.00087 kg/cm Lead = 11,350 kg/m = 0.01135 kg/cm Pressed wood = 190 kg/m = 0.00019 kg/cm

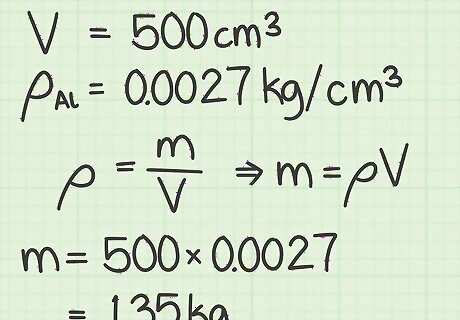
Multiply volume by density to find mass. Recall that the formula for density is Density = Mass Volume {\displaystyle {\text{Density}}={\frac {\text{Mass}}{\text{Volume}}}} {\text{Density}}={\frac {{\text{Mass}}}{{\text{Volume}}}}. Rearranging this to find the mass, the equation becomes Density ∗ Volume = Mass {\displaystyle {\text{Density}}*{\text{Volume}}={\text{Mass}}} {\text{Density}}*{\text{Volume}}={\text{Mass}}. Using the four sample materials, aluminum, butter, lead and pressed wood, find the mass of a sphere that has a volume of 500 cm. Aluminum : 500 cm 3 ∗ 0.0027 kg cm 3 = 1.35 kg {\displaystyle {\text{Aluminum}}:500{\text{ cm}}^{3}*0.0027{\frac {\text{kg}}{{\text{cm}}^{3}}}=1.35{\text{ kg}}} {\text{Aluminum}}:500{\text{ cm}}^{3}*0.0027{\frac {{\text{kg}}}{{\text{cm}}^{3}}}=1.35{\text{ kg}} Butter : 500 cm 3 ∗ 0.00087 kg cm 3 = 0.435 kg {\displaystyle {\text{Butter}}:500{\text{ cm}}^{3}*0.00087{\frac {\text{kg}}{{\text{cm}}^{3}}}=0.435{\text{ kg}}} {\text{Butter}}:500{\text{ cm}}^{3}*0.00087{\frac {{\text{kg}}}{{\text{cm}}^{3}}}=0.435{\text{ kg}} Lead : 500 cm 3 ∗ 0.01135 kg cm 3 = 5.675 kg {\displaystyle {\text{Lead}}:500{\text{ cm}}^{3}*0.01135{\frac {\text{kg}}{{\text{cm}}^{3}}}=5.675{\text{ kg}}} {\text{Lead}}:500{\text{ cm}}^{3}*0.01135{\frac {{\text{kg}}}{{\text{cm}}^{3}}}=5.675{\text{ kg}} Pressed wood : 500 cm 3 ∗ 0.00019 kg cm 3 = 0.095 kg {\displaystyle {\text{Pressed wood}}:500{\text{ cm}}^{3}*0.00019{\frac {\text{kg}}{{\text{cm}}^{3}}}=0.095{\text{ kg}}} {\text{Pressed wood}}:500{\text{ cm}}^{3}*0.00019{\frac {{\text{kg}}}{{\text{cm}}^{3}}}=0.095{\text{ kg}}

Solving a Sample Problem

Read the problem carefully. When answering problems about mass calculations, you need to read the full problem carefully. As you read, it may help to highlight the given data. Read the whole problem carefully to see what you are being asked to solve. For example, consider the following problem: A large sphere made of solid brass has a diameter of 1.2 m. Find the mass of the sphere.

Identify the known and unknown data. Reading the problem carefully, you should identify that you are given the diameter, so you will use the adjusted formula: Volume = 4 3 π ( d 2 ) 3 {\displaystyle {\text{Volume}}={\frac {4}{3}}\pi ({\frac {d}{2}})^{3}} {\text{Volume}}={\frac {4}{3}}\pi ({\frac {d}{2}})^{3} You should also notice that the sphere is made of brass. You will need to look up the density of brass from a density table online. From the website, EngineeringToolbox.com, you can find that the density of brass is 8480 kg/m. Because the diameter of the sphere was given in meters, its volume will be calculated in cubic meters, so you do not need to convert the density.

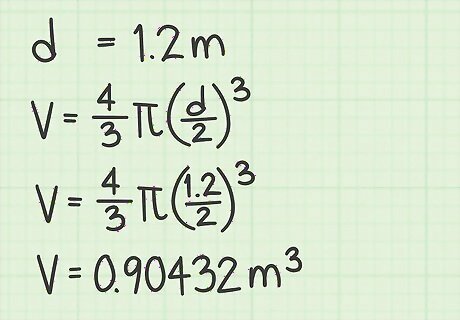
Calculate the volume. To calculate the volume, set up the correct formula, fill in the data you know and perform the calculations as follows: Volume = 4 3 π ( d 2 ) 3 {\displaystyle {\text{Volume}}={\frac {4}{3}}\pi ({\frac {d}{2}})^{3}} {\text{Volume}}={\frac {4}{3}}\pi ({\frac {d}{2}})^{3} Volume = 4 3 π ( 1.2 2 ) 3 {\displaystyle {\text{Volume}}={\frac {4}{3}}\pi ({\frac {1.2}{2}})^{3}} {\text{Volume}}={\frac {4}{3}}\pi ({\frac {1.2}{2}})^{3} Volume = 4.18667 ∗ 0.6 3 {\displaystyle {\text{Volume}}=4.18667*0.6^{3}} {\text{Volume}}=4.18667*0.6^{3} Volume = 4.18667 ∗ 0.216 {\displaystyle {\text{Volume}}=4.18667*0.216} {\text{Volume}}=4.18667*0.216 Volume = 0.90432 m 3 {\displaystyle {\text{Volume}}=0.90432{\text{ m}}^{3}} {\text{Volume}}=0.90432{\text{ m}}^{3}

Use the density to calculate the mass. Recall that Mass = Density ∗ Volume {\displaystyle {\text{Mass}}={\text{Density}}*{\text{Volume}}} {\text{Mass}}={\text{Density}}*{\text{Volume}}. Insert the values that you know to find the mass: Mass = Density ∗ Volume {\displaystyle {\text{Mass}}={\text{Density}}*{\text{Volume}}} {\text{Mass}}={\text{Density}}*{\text{Volume}} Mass = 8480 kg m 3 ∗ 0.90432 m 3 {\displaystyle {\text{Mass}}=8480{\frac {\text{ kg}}{{\text{ m}}^{3}}}*0.90432{\text{ m}}^{3}} {\text{Mass}}=8480{\frac {{\text{ kg}}}{{\text{ m}}^{3}}}*0.90432{\text{ m}}^{3} Mass = 7668.6 kg {\displaystyle {\text{Mass}}=7668.6{\text{ kg}}} {\text{Mass}}=7668.6{\text{ kg}}