
views
Identifying Components by Graphing
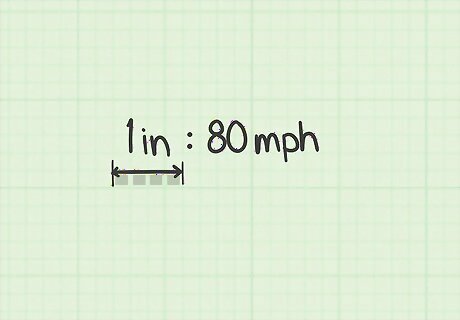
Select an appropriate scale. To graph the vector and its components, you need to decide on a scale for your graph. You need to choose a scale that is large enough to work with comfortably and accurately, but small enough that your vector can be drawn to scale. For example, suppose you're starting with a vector that represents a speed of 200 mph (320 km/h) in a northeasterly direction. If you're using graph paper with 4 squares per inch, you might choose to have each square represent 20 mph (32.2 km/h). This represents a scale of 1 inch (2.5 cm) = 80 mph. The vector’s placement with respect to the origin is irrelevant, so there's no need to draw an x-axis and y-axis. You're only measuring the vector itself, not its location in 2-dimensional or 3-dimensional space. The graph paper is just a measuring tool, so location doesn't matter.
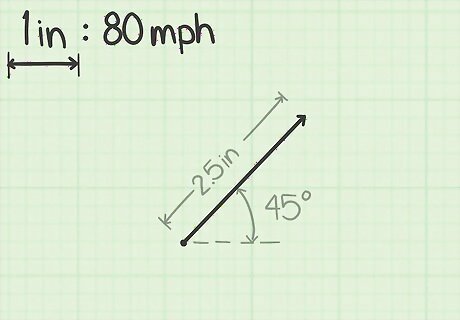
Draw the vector to scale. It is important that you sketch your vector as accurately as possible. You need to represent both the correct direction and length of the vector in your drawing. Use an accurate ruler. For example, if you've chosen the scale of one square on your graph paper representing 20 mph (32.2 km/h), and each square is ⁄4 inch (0.6 cm), then a vector of 200 mph (320 km/h) will be a line that is 10 squares, or 2 1/2 inches, long. Use a protractor, if necessary, to show the angle or direction of the vector. For example, if the vector shows movement in the northeast direction, draw a line at a 45-degree angle from the horizontal. The vector's can indicate many different kinds of direction measurements. If you're discussing travel, it might mean a direction on the map. To depict the path of a thrown or hit object, the vector's angle might mean the angle of travel from the ground. In nuclear physics, a vector might indicate an electron's direction.
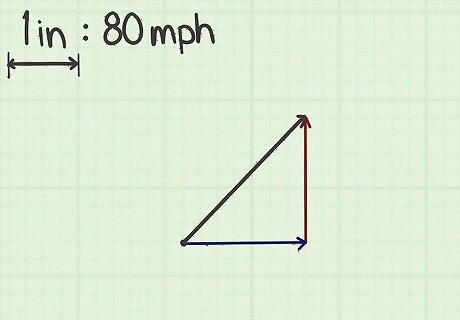
Draw a right triangle, with the vector as hypotenuse. Using your ruler, begin at the tail of the vector and draw a horizontal line as wide as necessary to coincide with the head of the vector. Mark an arrowhead at the tip of that line to indicate that this is also a component vector. Then draw a vertical line from that point to the head of the original vector. Mark an arrowhead at this point as well. You should have created a right triangle, consisting of 3 vectors. The original vector is the hypotenuse of the right triangle. The base of the right triangle is a horizontal vector, and the height of the right triangle is a vertical vector. There are 2 exceptions when you can't construct a right triangle. This will occur when the original vector is either exactly horizontal or vertical. For a horizontal vector, the vertical component is zero, and for a vertical vector, the horizontal component is zero.
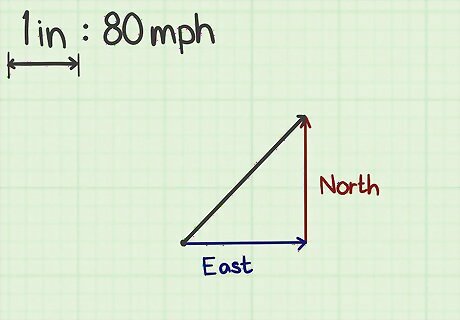
Label the two component vectors. Depending on what is being represented by your original vector, you should label the two component vectors that you have just drawn. For example, using the vector that represents travel in a northeasterly direction, the horizontal vector represents “East,” and the vertical vector represents “North.” Other samples of components might be “Up/Down” or “Left/Right.”
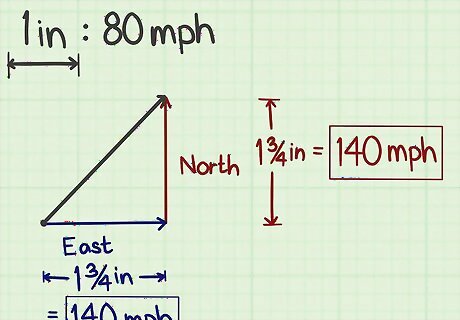
Measure the component vectors. You can determine the magnitudes of your 2 component vectors using either the graph paper alone or a ruler. If you use a ruler, then measure the length of each of the component vectors and convert using the scale you have selected. For example, a horizontal line that is 1 ⁄4 inches (3.2 cm) long, using a scale of 1 inch (2.5 cm) = 80 mph., would represent an easterly component of 100 mph (160 km/h). If you choose to rely on the graph paper rather than a ruler, you may need to estimate a bit. If your line crosses 3 full squares on the graph paper and falls in the middle of the 4th square, you would need to estimate the fraction of that last square and multiply by your scale. For example, if 1 square = 20 mph (32.2 km/h), and you estimate that a component vector is 3 1/2 squares, then that vector represents 70 mph. Repeat the measurement for both the horizontal and vertical component vectors, and label your results.
Calculating Components with Trigonometry

Construct a rough sketch of the original vector. By relying on mathematical calculations, your graph does not need to be as neatly drawn. You do not need to determine any measurement scale. Just sketch a ray in the general direction of your vector. Label your sketched vector with its magnitude and the angle that it makes from the horizontal. For example, consider a rocket that's being fired upwards at a 60-degree angle, at a velocity of 1,500 meters (5,000 ft) per second. You would sketch a ray that points diagonally upward. Label its length “1500 m/s” and label its base angle “60°.” The diagram shown above indicates a force vector of 5 Newtons at an angle of 37 degrees from the horizontal.
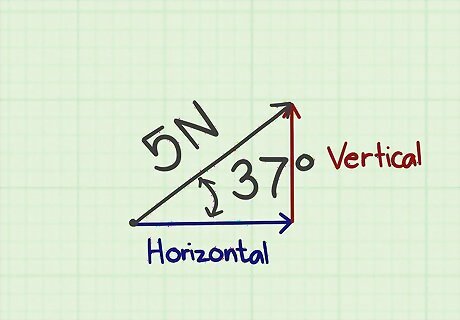
Sketch and label the component vectors. Sketch a horizontal ray beginning at the base of your original vector, pointing in the same direction (left or right) as the original. This represents the horizontal component of the original vector. Sketch a vertical ray that connects the head of your horizontal vector to the head of your original angled vector. This represents the vertical component of the original vector. A vector's horizontal and vertical components represent a theoretical, mathematical way of breaking a force into 2 parts. Imagine the child's toy Etch-a-Sketch, with the separate "Vertical" and "Horizontal" drawing knobs. If you drew a line using only the "Vertical" knob and then followed with a line using only the "Horizontal" knob, you would end at the same spot as if you had turned both knobs together at exactly the same speeds. This illustrates how a horizontal and vertical force can act simultaneously on an object.

Use the sine function to calculate the vertical component. Because the components of a vector create a right triangle, you can use trigonometric calculations to get precise measurements of the components. Use the equation: sin θ = vertical hypotenuse {\displaystyle \sin \theta ={\frac {\text{vertical}}{\text{hypotenuse}}}} \sin \theta ={\frac {{\text{vertical}}}{{\text{hypotenuse}}}} For the missile example, you can calculate the vertical component by substituting the values that you know, and then simplifying, as follows: sin θ = vertical hypotenuse {\displaystyle \sin \theta ={\frac {\text{vertical}}{\text{hypotenuse}}}} \sin \theta ={\frac {{\text{vertical}}}{{\text{hypotenuse}}}} sin ( 60 ) = vertical 1500 {\displaystyle \sin(60)={\frac {\text{vertical}}{1500}}} \sin(60)={\frac {{\text{vertical}}}{1500}} 1500 sin ( 60 ) = vertical {\displaystyle 1500\sin(60)={\text{vertical}}} 1500\sin(60)={\text{vertical}} 1500 ∗ 0.866 = vertical {\displaystyle 1500*0.866={\text{vertical}}} 1500*0.866={\text{vertical}} 1 , 299 {\displaystyle 1,299} 1,299 Label your result with the appropriate units. In this case, the vertical component represents an upward speed of 1,299 meters (4,000 ft) per second. The diagram above shows an alternate example, calculating the components of a force of 5 Newtons at a 37 degree angle. Using the sine function, the vertical force is calculated to be 3 Newtons.
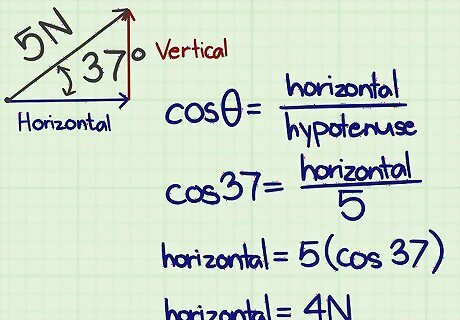
Use the cosine function to calculate the horizontal component. In the same way that you use sine to calculate the vertical component, you can use cosine to find the magnitude of the horizontal component. Use the equation: cos θ = horizontal hypotenuse {\displaystyle \cos \theta ={\frac {\text{horizontal}}{\text{hypotenuse}}}} \cos \theta ={\frac {{\text{horizontal}}}{{\text{hypotenuse}}}} Use the details from the missile example to find its horizontal component as follows: cos θ = horizontal hypotenuse {\displaystyle \cos \theta ={\frac {\text{horizontal}}{\text{hypotenuse}}}} \cos \theta ={\frac {{\text{horizontal}}}{{\text{hypotenuse}}}} cos ( 60 ) = horizontal 1500 {\displaystyle \cos(60)={\frac {\text{horizontal}}{1500}}} \cos(60)={\frac {{\text{horizontal}}}{1500}} 1500 cos ( 60 ) = horizontal {\displaystyle 1500\cos(60)={\text{horizontal}}} 1500\cos(60)={\text{horizontal}} 1500 ∗ 0.5 = horizontal {\displaystyle 1500*0.5={\text{horizontal}}} 1500*0.5={\text{horizontal}} 750 {\displaystyle 750} 750 Label your result with the appropriate units. In this case, the horizontal component represents a forward (or left, right, backward) speed of 750 meters (2,000 ft) per second. The diagram above shows an alternate example, calculating the components of a force of 5 Newtons at a 37 degree angle. Using the cosine function, the horizontal force is calculated to be 4 Newtons.
Using Vector Components to Add Vectors
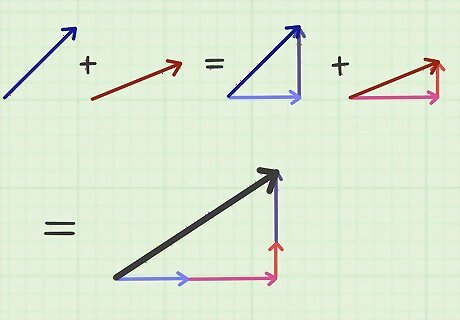
Understand what “adding” vectors means. Addition is generally a fairly simple concept, but it takes on special meaning when working with vectors. A single vector represents a movement, a force, or some other physical element acting upon an object. If there are two or more forces acting at the same time, you can “add” these forces to find the resultant force acting on the object. For example, think of a golf ball that's hit into the air. One force acting on the ball is the force of the initial hit, and it consists of an angle and magnitude. Another force might be the wind, which has its own angle and magnitude. Adding these 2 forces can describe the resulting travel of the ball.
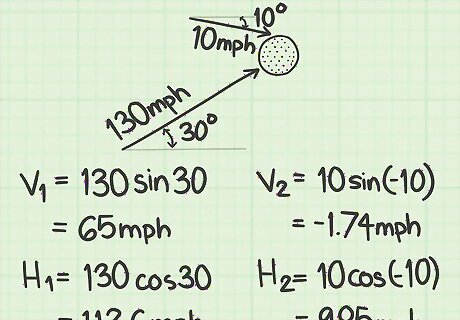
Break each vector into its component parts. Before you can add the vectors, you need to determine the components of each one. Using either of the processes described in this article, find the horizontal and vertical components of each force. For example, suppose the golf ball is hit at a 30-degree angle upward with a speed of 130 mph (210 km/h). Using trigonometry, the 2 component vectors are, therefore: Vertical = 130 sin ( 30 ) = 65 mph {\displaystyle {\text{Vertical}}=130\sin(30)=65{\text{mph}}} {\text{Vertical}}=130\sin(30)=65{\text{mph}} Horizontal = 130 cos ( 30 ) = 112.6 mph {\displaystyle {\text{Horizontal}}=130\cos(30)=112.6{\text{mph}}} {\text{Horizontal}}=130\cos(30)=112.6{\text{mph}} Then consider the vector that represents the force of the wind. Suppose the wind is blowing the ball downward at an angle of 10 degrees, at speed of 10 mph (16.1 km/h). (We are ignoring left and right forces for simplicity of calculation). The wind’s two components can be calculated similarly: Vertical = 10 sin ( − 10 ) = − 1.74 mph {\displaystyle {\text{Vertical}}=10\sin(-10)=-1.74{\text{mph}}} {\text{Vertical}}=10\sin(-10)=-1.74{\text{mph}} Horizontal = 10 cos ( − 10 ) = 9.85 mph {\displaystyle {\text{Horizontal}}=10\cos(-10)=9.85{\text{mph}}} {\text{Horizontal}}=10\cos(-10)=9.85{\text{mph}} Notice that we use an angle of -10 degrees because the wind is blowing down, acting against the force of the hit.

Add the components. Because the component vectors are always measured at right angles, you can add them directly. Pay attention matching the horizontal component of 1 vector to the horizontal component of the other, and the same for the vertical components. For this sample, the resultant vertical vector is the sum of the two components: Vertical = 65 + ( − 1.74 ) = 63.26 {\displaystyle {\text{Vertical}}=65+(-1.74)=63.26} {\text{Vertical}}=65+(-1.74)=63.26 Horizontal = 112.6 + 9.85 = 122.45 {\displaystyle {\text{Horizontal}}=112.6+9.85=122.45} {\text{Horizontal}}=112.6+9.85=122.45 Interpret the meaning of these results. The net force acting on the golf ball, due to both the hit and the wind, is the equivalent of a single force with components of 63.26 mph (101.81 km/h) vertically and 122.45 miles per hour horizontally.

Use the Pythagorean Theorem to find the magnitude of the resultant vector. Ultimately, what you would like to know is the net effect of both the golf swing and the wind, acting together on the ball. If you know the two components, you can put them together with the Pythagorean theorem to find the magnitude of the resultant vector. Recall that the component vectors represent the legs of a right triangle. The resultant vector is the hypotenuse of that right triangle. Using the Pythagorean theorem, c 2 = a 2 + b 2 {\displaystyle c^{2}=a^{2}+b^{2}} c^{2}=a^{2}+b^{2}, you can calculate this as follows: Resultant 2 = 63.26 2 + 122.45 2 {\displaystyle {\text{Resultant}}^{2}=63.26^{2}+122.45^{2}} {\text{Resultant}}^{2}=63.26^{2}+122.45^{2} Resultant 2 = 18 , 995.83 {\displaystyle {\text{Resultant}}^{2}=18,995.83} {\text{Resultant}}^{2}=18,995.83 Resultant = 18 , 995.83 {\displaystyle {\text{Resultant}}={\sqrt {18,995.83}}} {\text{Resultant}}={\sqrt {18,995.83}} Resultant = 137.83 {\displaystyle {\text{Resultant}}=137.83} {\text{Resultant}}=137.83 Thus, the resultant vector represents a single force on the ball with a magnitude of 137.83 mph (221.82 km/h). Notice that this is slightly higher than the force of the initial hit, because the wind is pushing the ball forward at the same time that it pushes it down.

Use trigonometry to find the angle of the resultant vector. Knowing the force of the resultant vector is half of the solution. The other half is to find the net angle of the resultant vector. In this example, because the golf swing applies an upward force and the wind applies a downward, though lesser, force, you need to find the resulting angle. Sketch a right triangle and label the component parts. The horizontal base of the triangle represents the forward vector component of 122.45. The vertical leg represents the upward vector component of 63.26. The hypotenuse represents the resultant vector with a magnitude of 137.83. You can choose either the sine function, with the vertical component, or the cosine function, with the horizontal component, to find the angle. The result will be the same. sin θ = 63.26 137.83 {\displaystyle \sin \theta ={\frac {63.26}{137.83}}} \sin \theta ={\frac {63.26}{137.83}} sin θ = 0.459 {\displaystyle \sin \theta =0.459} \sin \theta =0.459 θ = arcsin ( 0.459 ) {\displaystyle \theta =\arcsin(0.459)} \theta =\arcsin(0.459) θ = 27.32 {\displaystyle \theta =27.32} \theta =27.32 Thus, the resultant vector represents a single force acting on the ball at an upward angle of 27.32 degrees. This makes sense, as it's slightly lower than the swing's angle, at 30 degrees, due to the downward force of the wind. However, the golf swing is a much stronger force than the wind in this example, so the angle is still close to 30.

Summarize your resultant vector. To report the resultant vector, give both its angle and magnitude. In the golf ball example, the resultant vector has a magnitude of 137.83 mph (221.82 km/h), at an angle of 27.32 degrees above the horizontal.
Reviewing Vectors and Their Components
Recall the definition of a vector. A vector is a mathematical tool that is used in physics to represent the way forces act on an object. A vector is said to represent two elements of the force, its direction and its magnitude. For example, you can describe a moving object's movement by giving the direction of its travel and speed. You might say a plane is moving in a northwest direction at 500 mph (800 km/h). Northwest is the direction, and 500 mph (800 km/h) is the magnitude. A dog being held on a leash experiences a vector force. The leash held by the owner is being pulled diagonally upward with some measure of force. The angle of the diagonal is the vector's direction, and the strength of the force is the magnitude.

Understand the terminology of graphing vectors. When you draw a vector, either using a precisely drawn representation on graph paper or just a rough sketch, certain geometrical terms are used. A vector is represented graphically by a ray {\displaystyle {\text{ray}}} {\text{ray}}. A ray, in geometry, is a line segment that begins at one point and, theoretically, continues infinitely in some direction. A ray is drawn by marking a point, then a line segment of appropriate length, and marking an arrowhead at the opposite end of the line segment. The tail {\displaystyle {\text{tail}}} {\text{tail}} of a vector is its starting point. Geometrically, this is the endpoint of the ray. The head {\displaystyle {\text{head}}} {\text{head}} of a vector is the position of the arrowhead. The difference between a geometric ray and a vector is that the ray's arrowhead represents theoretical travel of infinite distance in the given direction. A vector, however, uses the arrowhead to indicate direction, but the length of the vector ends at the tip of the line segment, to measure its magnitude. In other words, if you sketch a ray in geometry, the length is irrelevant. If you draw a vector, however, the length is very important.

Recall some basic trigonometry. Component parts of a vector rely on the trigonometry of right triangles. Any diagonal line segment can become the hypotenuse of a right triangle by sketching a horizontal line from one end and a vertical line from the other end. When those two lines meet, you will have defined a right triangle. The reference angle is the angle that is made by measuring from the horizontal base of the right triangle to the hypotenuse. The sine of the reference angle can be determined by dividing the length of the opposite leg by the length of the hypotenuse. The cosine of the reference angle can be determined by dividing the length of the base of the triangle (or the adjacent leg) by the length of the hypotenuse.




















Comments
0 comment