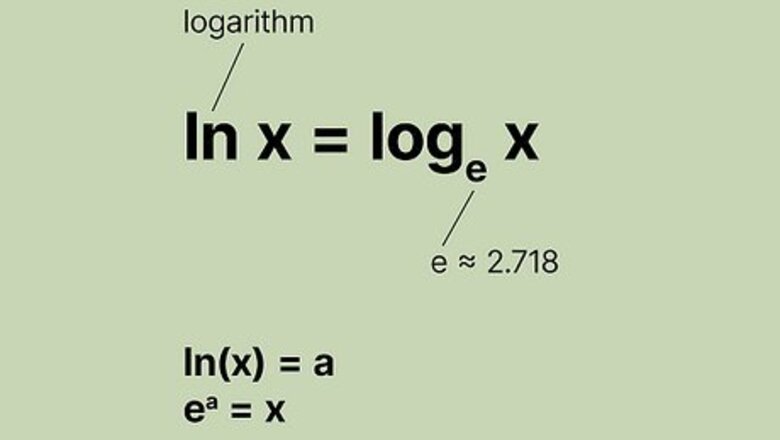
views
- The natural log, denoted as , is a logarithm with the base
- and are inverse functions, so raise to the base of to get rid of
- To solve an equation with , isolate to 1 side. Combine any natural logs together. Then, exponentiate each side with to cancel out .
What is ln?
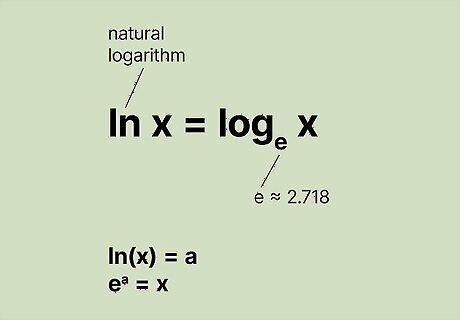
Natural log, written as l n {\displaystyle ln} {\displaystyle ln}, is a logarithm that uses the base of e {\displaystyle e} e. A logarithm is the inverse of an exponent. It tells you what a base number has to be raised to in order to produce another number. Natural logs, written as l n {\displaystyle ln} {\displaystyle ln} always use the base number e {\displaystyle e} e, which is an irrational number that is approximately equal to 2.718. In simpler terms, logs and natural logs ask what exponent produced the answer. Because logs and exponents are inverses of each other, writing l o g 2 ( 8 ) = 3 {\displaystyle log2(8)=3} {\displaystyle log2(8)=3} is the same thing as writing 2 3 = 8 {\displaystyle 2^{3}=8} 2^{3}=8. The base of the logarithm is 2, which is raised to the power of 3 to produce 8. Using a natural log example, l n ( 30 ) = 3.4012 {\displaystyle ln(30)=3.4012} {\displaystyle ln(30)=3.4012} is another way of writing e 3.4012 = 30 {\displaystyle e^{3.4012}=30} {\displaystyle e^{3.4012}=30}. The base e {\displaystyle e} e is raised to 3.4012 to produce 30.
Canceling Out ln
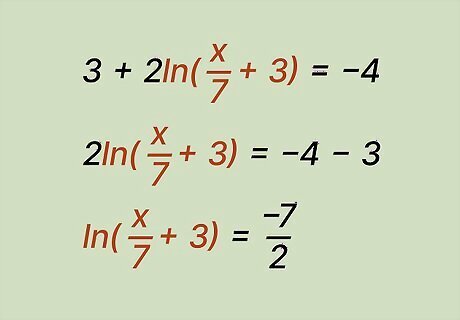
Isolate the natural log on 1 side of the equation. If your equation has multiple variables, move them around so the natural log is by itself on one side. In equations with multiple natural logs, move them to the same side of the equation and combine them. For example, solve the equation 3 + 2 l n ( x 7 + 3 ) = − 4. {\displaystyle 3+2ln({\frac {x}{7}}+3)=-4.} {\displaystyle 3+2ln({\frac {x}{7}}+3)=-4.} Subtract the 3 to move it to the other side: 2 l n ( x 7 + 3 ) = − 7. {\displaystyle 2ln({\frac {x}{7}}+3)=-7.} {\displaystyle 2ln({\frac {x}{7}}+3)=-7.} Divide by 2 to fully isolate ln: l n ( x 7 + 3 ) = − 7 2 . {\displaystyle ln({\frac {x}{7}}+3)={\frac {-7}{2}}.} {\displaystyle ln({\frac {x}{7}}+3)={\frac {-7}{2}}.}
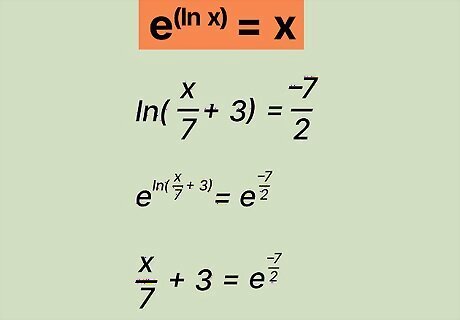
Exponentiate both sides of the equation with e {\displaystyle e} e to cancel out l n {\displaystyle ln} {\displaystyle ln}. To get rid of the natural log in an expression, simply raise each side of the equation to the base of e {\displaystyle e} e. L n {\displaystyle Ln} {\displaystyle Ln} and e {\displaystyle e} e cancel out, leaving you with a solvable expression. Using the simplified equation l n ( x 7 + 3 ) = − 7 2 {\displaystyle ln({\frac {x}{7}}+3)={\frac {-7}{2}}} {\displaystyle ln({\frac {x}{7}}+3)={\frac {-7}{2}}}: Exponentiate each side with e {\displaystyle e} e: e l n ( x 7 + 3 ) = e − 7 2 . {\displaystyle e^{ln({\frac {x}{7}}+3)}=e^{\frac {-7}{2}}.} {\displaystyle e^{ln({\frac {x}{7}}+3)}=e^{\frac {-7}{2}}.} Cancel out l n {\displaystyle ln} {\displaystyle ln}: x 7 + 3 = e − 7 2 . {\displaystyle {\frac {x}{7}}+3=e^{\frac {-7}{2}}.} {\displaystyle {\frac {x}{7}}+3=e^{\frac {-7}{2}}.}
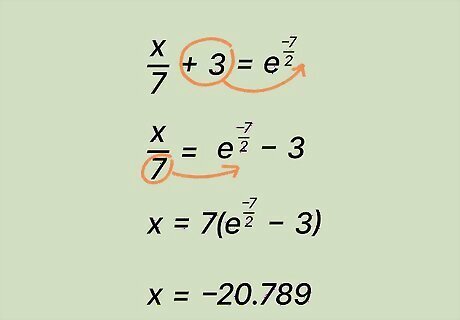
Solve the equation for x. With l n {\displaystyle ln} {\displaystyle ln} gone from the equation, solve it like normal. An e {\displaystyle e} e is often still in the equation, so follow your teacher’s directions to either leave it in the final solution, or simplify the answer in decimals. To get the answer in decimals, use a scientific calculator. Solve x 7 + 3 = e − 7 2 {\displaystyle {\frac {x}{7}}+3=e^{\frac {-7}{2}}} {\displaystyle {\frac {x}{7}}+3=e^{\frac {-7}{2}}}: Subtract 3 from both sides: x 7 = e − 7 2 − 3. {\displaystyle {\frac {x}{7}}=e^{\frac {-7}{2}}-3.} {\displaystyle {\frac {x}{7}}=e^{\frac {-7}{2}}-3.} Multiply 7 by both sides: x = 7 ( e − 7 2 − 3 ) . {\displaystyle x=7(e^{\frac {-7}{2}}-3).} {\displaystyle x=7(e^{\frac {-7}{2}}-3).} Leave the equation like this, or simplify. Round the answer to the nearest thousandth using a calculator: x = 7 ( e − 7 2 − 3 ) = − 20.789. {\displaystyle x=7(e^{\frac {-7}{2}}-3)=-20.789.} {\displaystyle x=7(e^{\frac {-7}{2}}-3)=-20.789.}
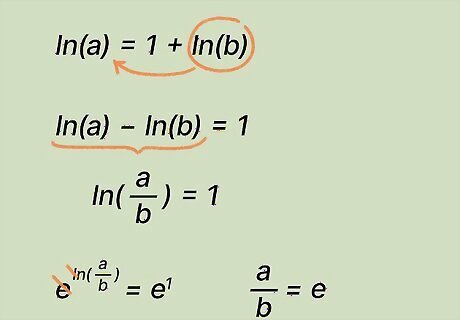
Practice getting rid of l n {\displaystyle ln} {\displaystyle ln} with multiple logs. In more complicated expressions, your equation might have more than 1 natural log. Just follow the same steps as above, making sure to combine the natural logs before you exponentiate. Solve the equation l n ( x − 1 ) = 1 + l n ( 3 x + 2 ) . {\displaystyle ln(x-1)=1+ln(3x+2).} {\displaystyle ln(x-1)=1+ln(3x+2).} Isolate l n {\displaystyle ln} {\displaystyle ln} to 1 side of the equation: l n ( x − 1 ) − l n ( 3 x + 2 ) = 1. {\displaystyle ln(x-1)-ln(3x+2)=1.} {\displaystyle ln(x-1)-ln(3x+2)=1.} Combine the natural logs together. In this equation, 2 logs are subtracted. So, combine them by dividing them by each other. l n ( x − 1 3 x + 2 ) = 1. {\displaystyle ln({\frac {x-1}{3x+2}})=1.} {\displaystyle ln({\frac {x-1}{3x+2}})=1.} Exponentiate both sides with e {\displaystyle e} e: e l n ( x − 1 3 x + 2 ) = e 1 . {\displaystyle e^{ln({\frac {x-1}{3x+2}})}=e^{1}.} {\displaystyle e^{ln({\frac {x-1}{3x+2}})}=e^{1}.} Cancel out l n {\displaystyle ln} {\displaystyle ln}: x − 1 3 x + 2 = e . {\displaystyle {\frac {x-1}{3x+2}}=e.} {\displaystyle {\frac {x-1}{3x+2}}=e.} Simplify and solve: x − 1 = e ( 3 x + 2 ) {\displaystyle x-1=e(3x+2)} {\displaystyle x-1=e(3x+2)} x − 1 = 3 e x + 2 e {\displaystyle x-1=3ex+2e} {\displaystyle x-1=3ex+2e} x − 1 − 3 e x = 2 e {\displaystyle x-1-3ex=2e} {\displaystyle x-1-3ex=2e} x − 3 e x = 2 e + 1 {\displaystyle x-3ex=2e+1} {\displaystyle x-3ex=2e+1} ( 1 − 3 e ) x = 2 e + 1 {\displaystyle (1-3e)x=2e+1} {\displaystyle (1-3e)x=2e+1} x = 2 e + 1 1 − 3 e {\displaystyle x={\frac {2e+1}{1-3e}}} {\displaystyle x={\frac {2e+1}{1-3e}}} Round the answer to the nearest thousandth: x = − 0.900. {\displaystyle x=-0.900.} {\displaystyle x=-0.900.}
Properties of ln and Logs
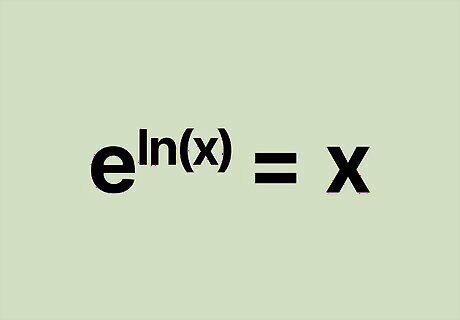
Logs and exponents are inverse functions that undo each other. Because natural logs and e {\displaystyle e} e are closely related, all you have to do is raise l n {\displaystyle ln} {\displaystyle ln} to the base of e {\displaystyle e} e to get rid of it. Similarly, if you have an equation with e {\displaystyle e} e, you take its natural log to cancel it out. For example, if you have l n ( x ) , {\displaystyle ln(x),} {\displaystyle ln(x),} you raise it to the base of e {\displaystyle e} e to get e l n ( x ) . {\displaystyle e^{ln(x)}.} {\displaystyle e^{ln(x)}.} The l n {\displaystyle ln} {\displaystyle ln} and e {\displaystyle e} e cancel out, leaving you with x {\displaystyle x} x.
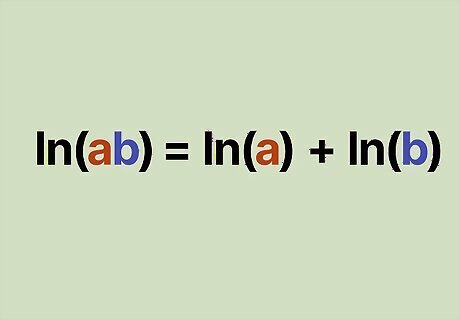
A log that is multiplied is the same as the sum of the logs. That might sound confusing, but this just means that when 2 terms in a log are multiplied, that’s the same as adding the log of the first term with the log of the second. Mathematically, this looks like l n ( a b ) = l n ( a ) + l n ( b ) . {\displaystyle ln(ab)=ln(a)+ln(b).} {\displaystyle ln(ab)=ln(a)+ln(b).} This relationship makes it easy to group and combine logs with the same base, like natural logs, when there are multiple logs in an equation. Be careful of confusing l n ( a b ) {\displaystyle ln(ab)} {\displaystyle ln(ab)} with l n ( a + b ) . {\displaystyle ln(a+b).} {\displaystyle ln(a+b).} l n ( a + b ) {\displaystyle ln(a+b)} {\displaystyle ln(a+b)} does not equal l n ( a ) + l n ( b ) . {\displaystyle ln(a)+ln(b).} {\displaystyle ln(a)+ln(b).}
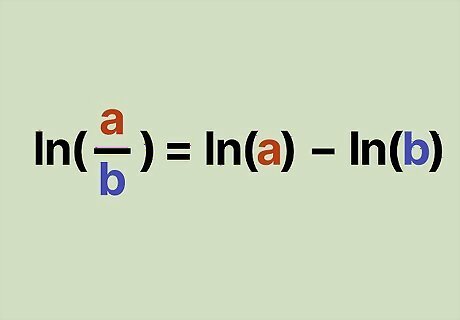
A log that is divided is the same as the difference of the logs. This relationship between logs is similar to logs that are multiplied. When 2 terms of a log with the same base are divided, that’s like subtracting the log of the second term from the log of the first term. This relationship is written as l n ( a b ) = l n ( a ) − l n ( b ) . {\displaystyle ln({\frac {a}{b}})=ln(a)-ln(b).} {\displaystyle ln({\frac {a}{b}})=ln(a)-ln(b).} Be aware that l n ( a − b ) {\displaystyle ln(a-b)} {\displaystyle ln(a-b)} is not the same as l n ( a ) − l n ( b ) {\displaystyle ln(a)-ln(b)} {\displaystyle ln(a)-ln(b)}. The terms have to be divided by each other in order to equal l n ( a ) − l n ( b ) {\displaystyle ln(a)-ln(b)} {\displaystyle ln(a)-ln(b)}.
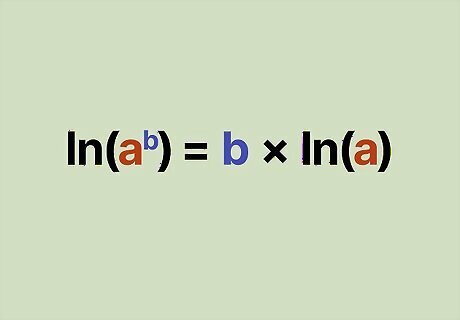
An exponential term in a log equals the exponent multiplied by the log. Some terms in a log have an exponent, which might look confusing at first. When you see them in an equation, that simply means that the exponent on the term in the log is the same as multiplying the exponent by the log. This is expressed like: l n ( a b ) = b ∗ l n ( a ) {\displaystyle ln(a^{b})=b*ln(a)} {\displaystyle ln(a^{b})=b*ln(a)}. A log raised to an exponent does not follow the same properties as a log with a term raised to an exponent. For example, ( l n ( a ) ) b {\displaystyle (ln(a))^{b}} {\displaystyle (ln(a))^{b}} does not equal b ∗ l n ( a ) . {\displaystyle b*ln(a).} {\displaystyle b*ln(a).}
Getting Rid of e
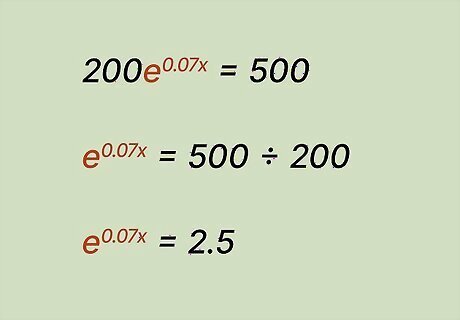
Move all expressions with e {\displaystyle e} e to 1 side of the equation. The good news is that getting rid of e {\displaystyle e} e follows a similar process as getting rid of l n {\displaystyle ln} {\displaystyle ln}. Start by isolating e {\displaystyle e} e to 1 side of the equation. For example, solve the equation 200 e 0.07 x = 500. {\displaystyle 200e^{0.07x}=500.} {\displaystyle 200e^{0.07x}=500.} Divide each side by 200: e 0.07 x = 500 200 . {\displaystyle e^{0.07x}={\frac {500}{200}}.} {\displaystyle e^{0.07x}={\frac {500}{200}}.} Simplify the fraction: e 0.07 x = 2.5. {\displaystyle e^{0.07x}=2.5.} {\displaystyle e^{0.07x}=2.5.}
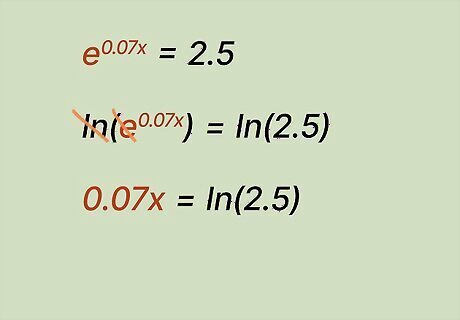
Take the natural log of both sides of the equation to cancel out e {\displaystyle e} e. Because e {\displaystyle e} e and l n {\displaystyle ln} {\displaystyle ln} are inverse functions, taking the natural log of e {\displaystyle e} e gets rid of it. This brings down the exponent, leaving you with a solvable equation. Using the simplified equation e 0.07 x = 2.5 {\displaystyle e^{0.07x}=2.5} {\displaystyle e^{0.07x}=2.5}: Take the natural log of both sides of the equation: l n ( e 0.07 x ) = l n ( 2.5 ) . {\displaystyle ln(e^{0.07x})=ln(2.5).} {\displaystyle ln(e^{0.07x})=ln(2.5).} Cancel out e {\displaystyle e} e and bring down its exponent: 0.07 x = l n ( 2.5 ) . {\displaystyle 0.07x=ln(2.5).} {\displaystyle 0.07x=ln(2.5).}
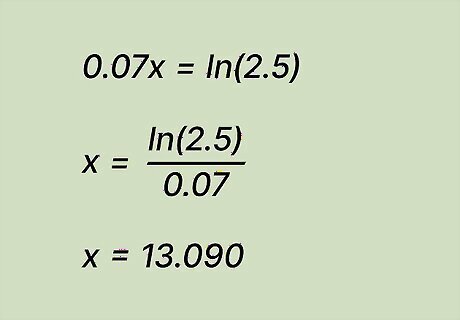
Solve the equation for x. Now that e {\displaystyle e} e is out of the equation, simplify and solve the equation like normal. It’s likely that a natural log will still be in your equation, so follow your teacher’s instructions to either keep l n {\displaystyle ln} {\displaystyle ln} in the answer, or use a calculator to get a numerical answer for x. Solve 0.07 x = l n ( 2.5 ) . {\displaystyle 0.07x=ln(2.5).} {\displaystyle 0.07x=ln(2.5).} Divide 0.07 by both sides: x = l n ( 2.5 ) 0.07 {\displaystyle x={\frac {ln(2.5)}{0.07}}} {\displaystyle x={\frac {ln(2.5)}{0.07}}} Use a calculator to round the answer to the nearest thousandth place: x = 13.090. {\displaystyle x=13.090.} {\displaystyle x=13.090.}



















Comments
0 comment