44
views
views
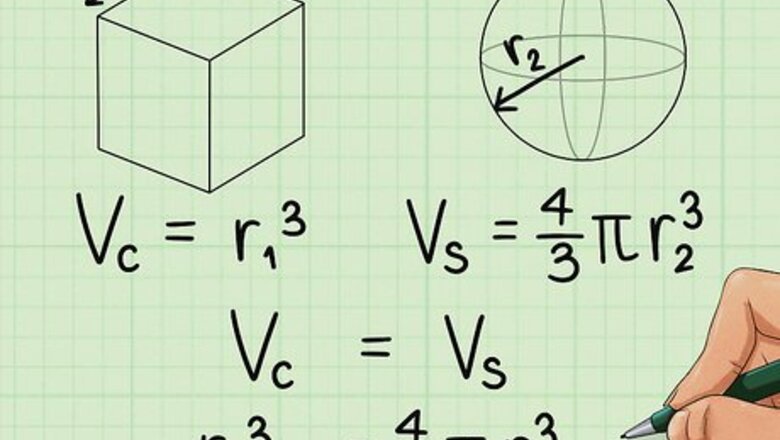
In this article r1 is used to represent the side of the cube and r2 to represent the radius of the sphere. The formula for the volume V of a cube c is s^3 where s = side (but here r is used for s) so r1^3 = V(c), and the volume of a sphere s is 4/3 πr^3, so in this example 4/3πr2^3 = V(s). The caret symbol, "^", denotes exponentiation for Microsoft Excel and the article will follow that syntax.
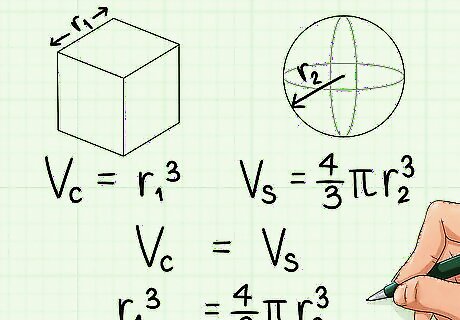
Set V(c) = V(s) via r1^3 = 4/3πr2^3

r1^3/r2^3 = 4/3π by dividing both sides by r2^3 and simplifying.
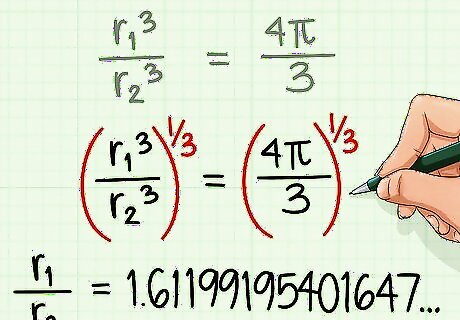
r1/r2 = (4/3π)^(1/3) = 1.61199195401647 by taking the cube root of both sides and evaluating the right side in Excel as "=(4/3*PI())^(1/3)"
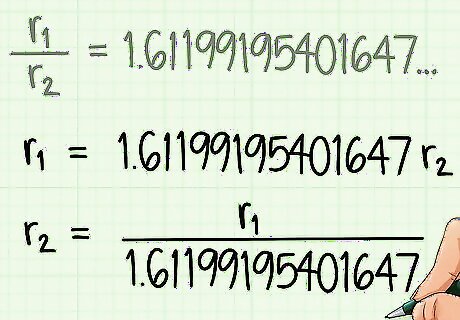
Now we can find either r1 or r2 given the other one, for r1 = r2 * 1.61199195401647 and r2 = r1 / 1.61199195401647, where r2 is the radius of the sphere and r1 is the side of the cube.
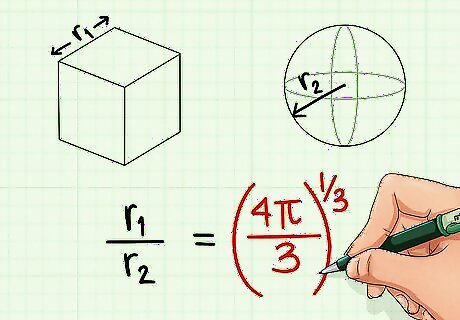
We now have also learned that (4/3π)^(1/3) MEANS the constant of proportion of the volume of a cube equal in volume to a sphere of different basis length r.

















Comments
0 comment