How to Calculate the Slope of a Line

• Slope = Rise divided by Run and is represented by the variable m. The slope m is found in the slope-intercept formula, y = mx + b
• When given two (x, y) points on a line, Run = x₂ - x₁ and Rise = y₂ - y₁. Therefore, m = (y₂ - y₁)/(x₂ - x₁).
• Find the slope by finding two (x, y) points on a line, labeling one (x₁, y₁) and the other (x₂, y₂). The slope m = (y₂ - y₁)/(x₂ - x₁).

Finding the Slope

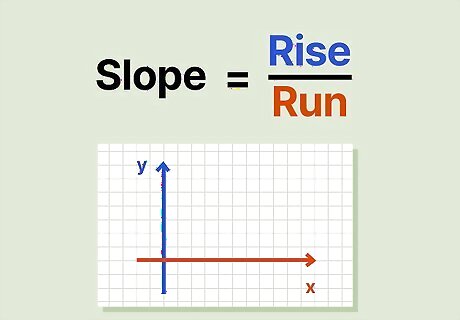
This is the slope formula, which states Slope = Rise over Run. When plotting a line on a graph, the “Rise” refers to the change in y that corresponds to a specific change in x. This change in x is called the “Run.” For instance, if y increases by 4 when x increases by 2, then Rise = 4 and Run = 2. To find the slope, divide 4/2 to get 2. The slope of a line is represented by the variable m. In this example, m = 2. The slope m is part of the formula y = mx + b. This is called the “slope-intercept formula.” You can use y = mx + b to calculate a value of y that corresponds to a particular value of x. Each pair of corresponding x and y values is called a “point”, written as (x, y). If you find multiple (x, y) points for the same equation, you can plot those points on a graph and draw a straight line through them.

Find two different points that the line passes through. Each point has an x value and a y value, written together as (x, y). You can pick any two points you like, as long as the line passes directly through them. In the example above, we picked the points (2, 1) and (5, 3). The first point has an x value of 2 and a y value of 1, so it’s written as (2, 1). The second point has an x value of 5 and a y value of 3. It’s written as (5, 3).

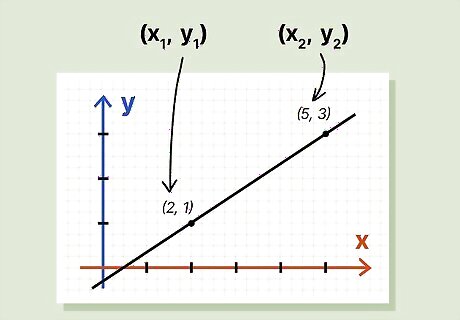
Choose one point to be (x1, y1) and the other to be (x2, y2). In other words, the first (x, y) pair can be (x1, y1), and the second paid can be (x2, y2). In the example above, (x1, y1) is (2, 1), while (x2, y2) is (5, 3). For simplicity, you can always make the point farthest on the left (x1, y1). This point will have the lower value for x. In reality, you can make either point (x1, y1) or (x2, y2), as long as you remember which is which.

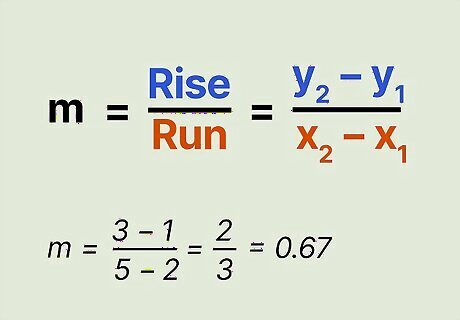
Calculate m by dividing the Rise by the Run. Rise = y2 - y1, while Run = x2 - x1. To illustrate this, let’s calculate m for our previous example using the coordinates (2, 1) and (5, 3): (x1, y1) = (2, 1), and (x2, y2) is (5, 3). Rise = y2 - y1, or 3 - 1. Run = x2 - x1, or 5 - 2. Rise/Run = (3 - 1)/(5 - 2), or (2/3). Therefore, m = ⅔, or 0.67.

Types of Slopes

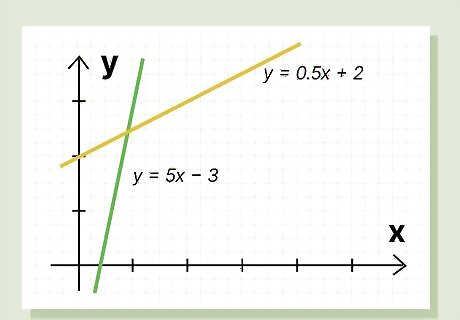
Positive slope: A positive slope is “uphill” with a positive m value. “Uphill” means that y increases as x increases. In the above image, the lines all have positive slopes. Note that each line goes uphill from left to right, and that the y value for each point gets larger as the x value gets larger. A positive slope can be a positive integer like 3, 5, or 16. It can also be a fraction or decimal, like ½, 0.75, or 1.86. Look closely at the y = mx + b formulas listed with each line. Notice that m is always a positive number.

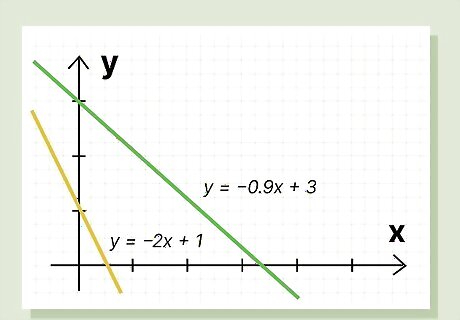
Negative slope: A negative slope is “downhill” with a negative m value. “Downhill” means that y decreases as x increases. In the above image, the lines all have negative slopes. Note that each line goes downhill from left to right, and that the y value for each point gets smaller as the x value gets larger. A negative slope can be a negative integer like -2, -6, or -19. It can also be a negative fraction or decimal, like -⅓, -0.9, or -2.21. Note the y = mx + b formulas for each line. You’ll see that m is always a negative number.

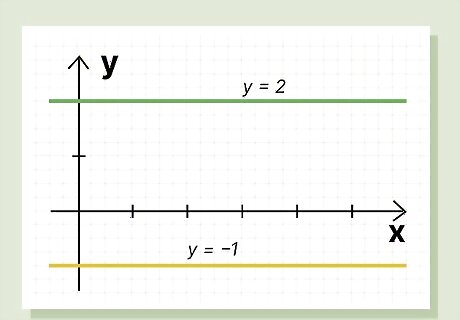
Zero slope: A horizontal line has a slope of m = 0. The y value always stays the same, even as x increases. In other words, the line doesn’t go “uphill” or “downhill”. In the graph above, you’ll see that all the lines are completely flat. A horizontal line always has a slope of m = 0. This means the equation y = mx + b can be written as y = 0x + b. Since 0x = 0, the equation gets simplified to y = b, with b being the y corresponding value for all values of x. The formulas for the line above all follow the same format: y = some number.

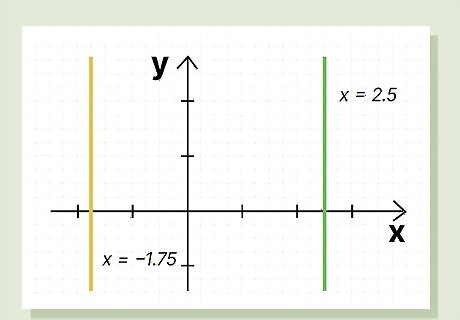
Undefined slope: A vertical line has an “undefined” slope and one value for x. In other words, y can have any value, but x always has the same value. Vertical lines can’t be written with the formula y = mx + b. Instead, they are written as x = some number, and the vertical line passes through the x-axis at that exact number. The image above shows lines with undefined slopes.